POLS 1600

Causal Inference in
Experimental Designs

Updated Mar 3, 2025

Overview

Class Plan

  • Announcements
  • Feedback
  • Review
  • Class plan
    • Causal Inference
    • Notation for Causal Inference
    • Causal Identification
    • Causal Identification in Experiments
    • resume data from QSS (Skipping, but their for your reference)
    • Explore Broockman and Kalla (2016)

Annoucements

  • We start taking attendance this week

  • Readings for this week:

    • QSS Chapter 2: pp. 38–65
    • Broockman and Kalla (2016)

  • No class next Tuesdays

  • No lab next Thursday

  • Meet your groups!

Group Assignments

 

Feedback

What did we like

 

What did we dislike

 

Setup

Every time you work in R

  • Save your file to your course or project folder

  • Set your working directory to where your file is saved

  • Load, and if needed, install packages

  • Maybe change some global options in your .Qmd file

Setting your working directory when working “Live”

Packages for today

## Pacakges for today
the_packages <- c(
  ## R Markdown
  "kableExtra","DT",
  
  ## Tidyverse
  "tidyverse", "lubridate", "forcats", 
  "haven", "labelled",
  
  ## Extensions for ggplot
  "ggmap","ggrepel", "ggridges", 
  "ggthemes", "ggpubr", "GGally",
  "scales", "dagitty", "ggdag", #<<
  
  # Data 
  "COVID19","maps","mapdata",
  "qss" #<<
)

## Define a function to load (and if needed install) packages

ipak <- function(pkg){
    new.pkg <- pkg[!(pkg %in% installed.packages()[, "Package"])]
    if (length(new.pkg)) 
        install.packages(new.pkg, dependencies = TRUE)
    sapply(pkg, require, character.only = TRUE)
}

## Install (if needed) and load libraries in the_packages
ipak(the_packages)
kableExtra         DT  tidyverse  lubridate    forcats      haven   labelled 
      TRUE       TRUE       TRUE       TRUE       TRUE       TRUE       TRUE 
     ggmap    ggrepel   ggridges   ggthemes     ggpubr     GGally     scales 
      TRUE       TRUE       TRUE       TRUE       TRUE       TRUE       TRUE 
   dagitty      ggdag    COVID19       maps    mapdata        qss 
      TRUE       TRUE       TRUE       TRUE       TRUE       TRUE

Review

Review: Data wrangling

Data transformations

You want to:

  • Load some data

  • Combine multiple functions

  • Look at your data

  • Recode your data

  • Transform your data

You could use

  • read_* functions

  • %>% the “pipe” operator

  • glimpse() head(), filter(), select(), arrange()

  • mutate(), case_when(), ifelse()

  • summarize(), group_by()

Data Visualization

  • The grammar of graphics

  • At minimum you need:

    • data
    • aesthetic mappings
    • geometries

  • Hey Jude, take a sad plot and make it better by:

    • labels
    • themes
    • statistics
    • cooridnates
    • facets
    • transforming your data before plotting

Practice

  • Create two variables x and y
    • x should be a random variable with 100 observations from a random normal (rnorm) distribution with mean 0 and standard deviation 1
    • y should be a function of x plus the square of a random normal distribution with mean 0 and standard deviation 1
  • Combine x and y into a data.frame called df
  • summarize the mean, median, standard deviation (sd), 16th and 84th percentile (quantile) of x and y and save this to an object called df_sum
  • Plot the distributions of x and y, separately, using a density plot (geom_density)
    • Add a rug to each density plot
    • Add vertical lines for the mean and median of each variable
    • A vertical lines at the 16th and and 84th percentile of each plot
      • Hint use your object df_sum as the data for these geometries

Practice

  • Tasks
  • Figures
  • Summary
  • Create two variables x and y
    • x should be a random variable with 100 observations from a random normal (rnorm) distribution with mean 0 and standard deviation 1
    • y should be a function of x plus the square of a random normal distribution with mean 0 and standard deviation 1
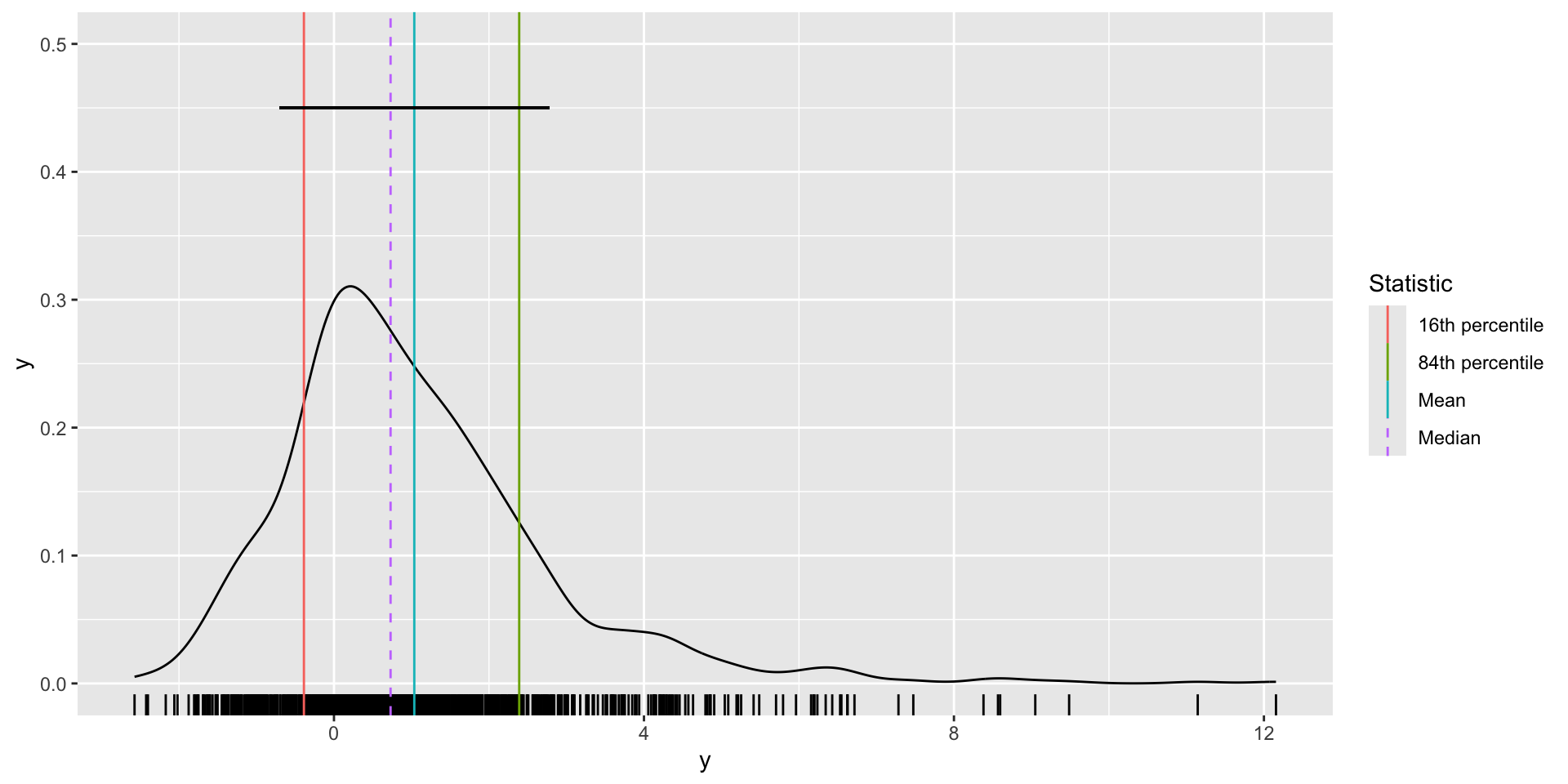
  • Combine x and y into a data.frame called df
  • summarize the mean, median, standard deviation (sd), 16th and 84th percentile (quantile) of x and y and save this to an object called df_sum
  • Plot the distributions of x and y, separately, using a density plot (geom_density)
    • Add a rug to each density plot
    • Add vertical lines for the mean and median of each variable
    • A vertical lines at the 16th and and 84th percentile of each plot
      • Hint: use your object df_sum as the data for these geometries
# Load libraries
library(tidyverse)

# Set seed for reproducibility
set.seed(123)

# Number of observations
n <- 1000

# Generate data
x <- rnorm(n, mean = 0, sd = 1)
y <- x + (rnorm(n, mean = 0, sd = 1))^2

# Create dataframe
df <- data.frame(x = x, y = y)

# Calculate summary statistics

df_sum <- df %>% 
  dplyr::summarise(
    x_mean = mean(x),
    x_median = median(x),
    x_sd = sd(x),
    x_16th = quantile(x, probs = .16),
    x_84th = quantile(x, probs = .84),
    y_mean = mean(y),
    y_median = median(y),
    y_sd = sd(y),
    y_16th = quantile(y, probs = .16),
    y_84th = quantile(y, probs = .84)
  )

df_sum
      x_mean    x_median     x_sd   x_16th    x_84th   y_mean  y_median
1 0.01612787 0.009209639 0.991695 -1.01607 0.9869428 1.036354 0.7302196
      y_sd     y_16th   y_84th
1 1.738673 -0.3879478 2.390059
fig_x <- df %>% 
  ggplot(aes(x))+
  geom_density()+
  geom_rug()+
  geom_vline(
    data = df_sum,
    aes(xintercept = x_mean, col="Mean"))+
  geom_vline(
    data = df_sum,
    aes(xintercept = x_median, col="Median"),
    linetype = "dashed")+
  geom_vline(
    data = df_sum,
    aes(xintercept = x_16th, col="16th percentile"))+
  geom_vline(
    data = df_sum,
    aes(xintercept = x_84th, col="84th percentile"))+
  geom_segment(
    aes(y=.45, yend=.45,
        x = df_sum$x_mean - df_sum$x_sd,
        xend = df_sum$x_mean + df_sum$x_sd)
  )+
  ylim(0,.5)+
  labs(
    col = "Statistic"
  )

fig_y <- df %>% 
  ggplot(aes(y))+
  geom_density()+
  geom_rug()+
  geom_vline(
    data = df_sum,
    aes(xintercept = y_mean, col="Mean"))+
  geom_vline(
    data = df_sum,
    aes(xintercept = y_median, col="Median"),
    linetype = "dashed")+
  geom_vline(
    data = df_sum,
    aes(xintercept = y_16th, col="16th percentile"))+
  geom_vline(
    data = df_sum,
    aes(xintercept = y_84th, col="84th percentile"))+
  geom_segment(
    aes(y=.45, yend=.45,
        x = df_sum$y_mean - df_sum$y_sd,
        xend = df_sum$y_mean + df_sum$y_sd)
  )+
  ylim(0,.5)+
  labs(
    col = "Statistic"
  )

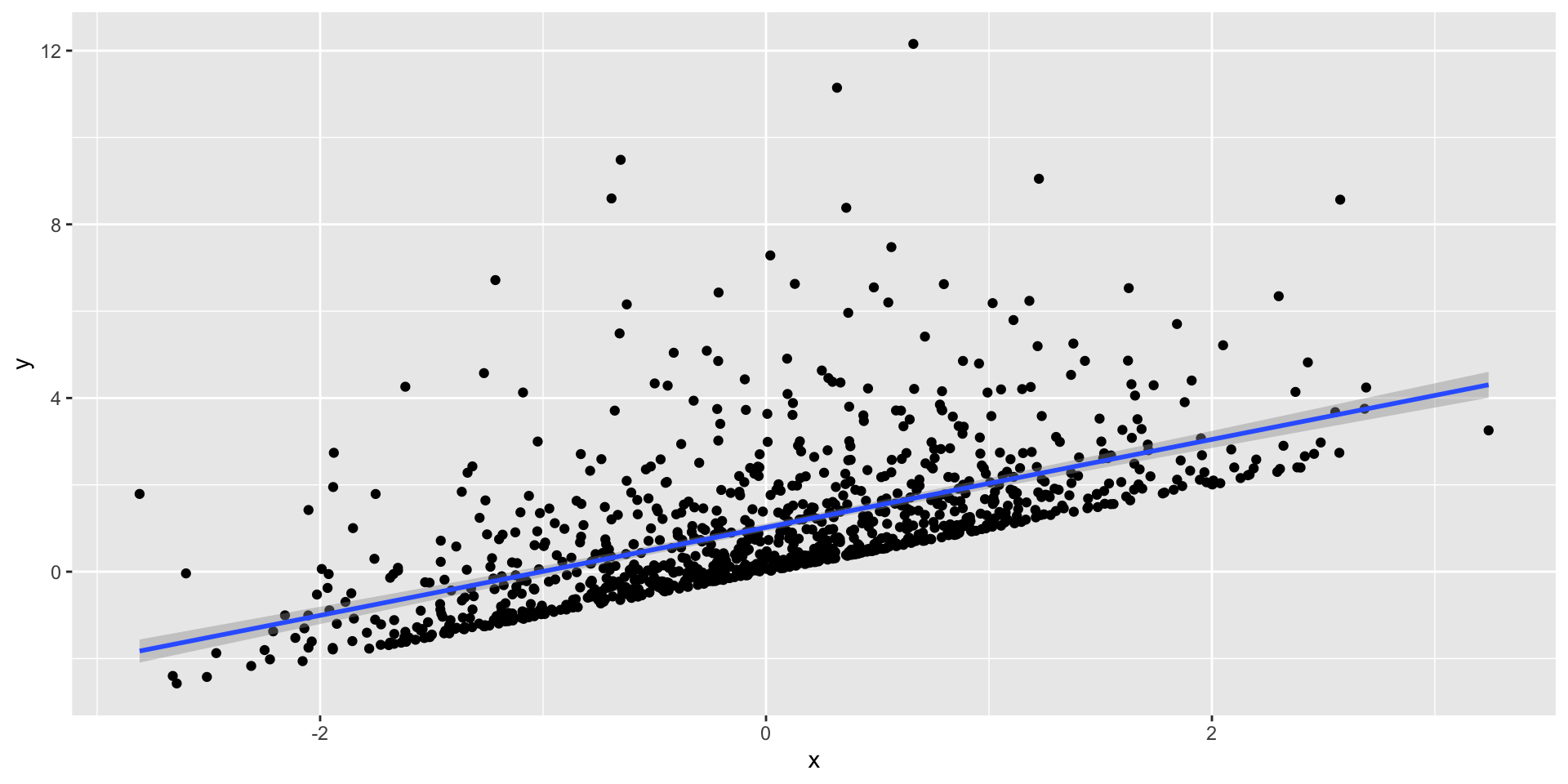
cor(df$x, df$y)
[1] 0.5779469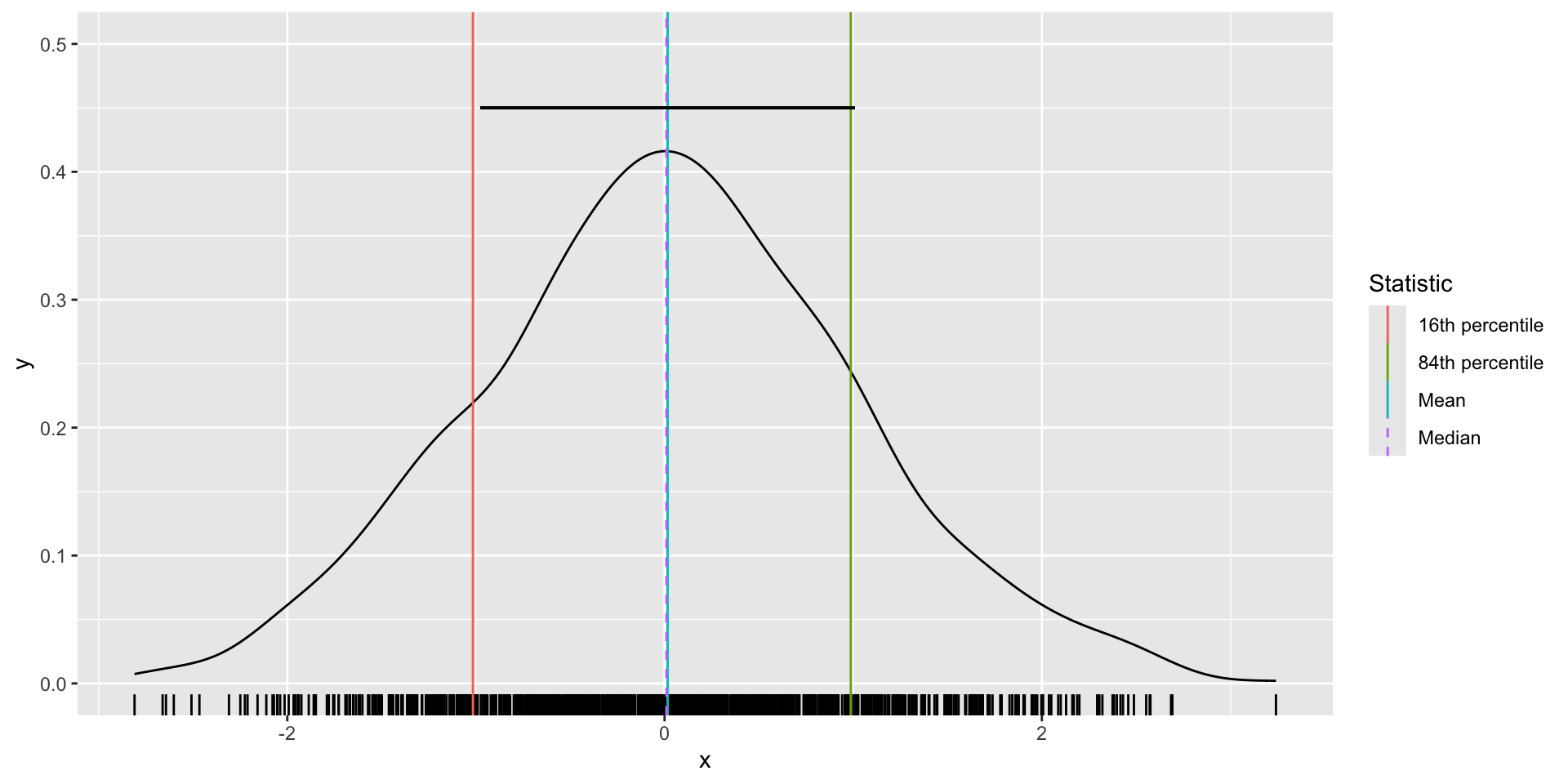
fig_xy <- df %>% 
  ggplot(aes(x,y))+
  geom_point()+
  geom_smooth(method="lm")

  • Measures of central tendency describe what’s typical

  • Measures of dispersion describe variation around what’s typical

Causal Inference

Causal claims imply counterfactual comparisons

  • Causal claims imply counterfactual comparisons

  • What would have happened if we were to change some aspect of the world?

What’s the counterfactual for these claims:

  • Foreign aid increases develop

  • Joe Rogan cost Kamala the 2024 election

  • Democracies don’t fight wars with other democracies

  • Universal Pre-K improves child development

Casual claims are all around us

Casual claims are all around us

What are some questions that interest you?

What are the counterfactual comparisons they imply?

Notation for Causal Inference

How to represent causal claims

In this course, we will use two forms of notation to describe our causal claims.

  • Directed Acyclic Graphs (DAGs, next lecture)

  • Potential Outcomes Notation

General Notation: Variables

  • Y our outcome of interest

  • D an indicator of treatment status

    • D=1 → treated
    • D=0 → not treated (control)

  • Z an of assignment status

    • Z=1 → assigned to treatment
    • Z=0 → assigned to control

  • X a covariate or predictor we can measure/observe

  • U unmeasured covariates

Expected Values

  • The E[Y] reads as “the expected value of Y”

  • E[Y] is defined as a probability weighted average based on the unconditional probability of Y ( f(y) )

E[Y]=∫−∞∞yf(y)dy

Conditional Expectations

  • The E[Y|X=x] reads as “the expected value of Y conditional on the value of X”

  • E[Y|X=x] is defined as a probability weighted average of Y based on the conditional probability of Y given X ( yfY|X(y|x) )

E[Y|X=x]=∫−∞∞yf(y|x)dy

Estimands, Estimators and Estimates

  • Estimand the thing we want to know.

    • Sometimes called a parameter (θ, “theta”) or quantity of interest
    • The expected value of heights in POLS 1600 (θ=E[X])

  • Estimator a rule or method for calculating an estimate of our estimand

    • An average of a sample of 10 student’s heights in POLS 1600
    • θ^=x¯=1/n∗∑1nxi

  • Estimate: a value produced by our estimator for some data

    • The average of our 10 person sample is 5'10''

Error and Bias

Formally, we’ll say an estimate, θ^ (“theta hat”) is an unbiased estimator of a parameter, θ (“theta”) if:

E[θ^]=θ

Bias or error, ϵ, is the difference between our estimate and the truth

ϵ=θ^−θ

An estimator is unbiased if, on average, the errors equal 0

E[ϵ]=E[θ^−θ]=0

Bias vs. variance

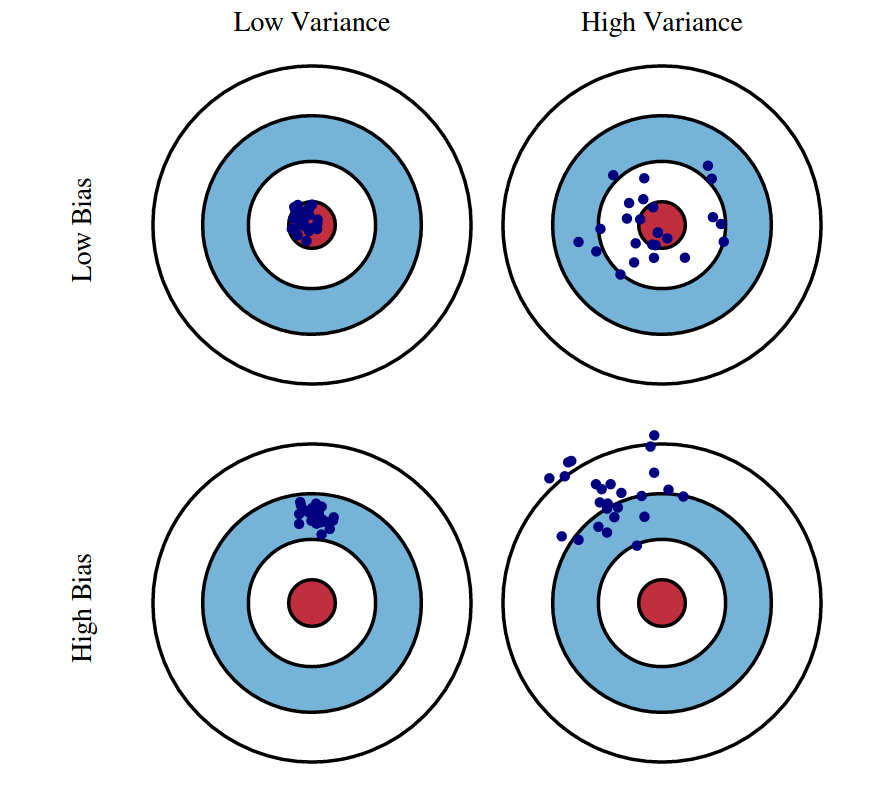
The bias-variance tradeoff

Potential outcomes notation

  • Yi(1) describes individual i’s outcome, Yi if they received the treatment (Di=1)
    • Shorthand for Yi(Di=1)
    • Paul’s Covid-19 status (Yi) with the vaccine (Di=1)
  • Yi(0) describes individual i’s outcome, Yi if they did not receive the treatment (Di=0)i
    • Shorthand for Yi(Di=0)
    • Paul’s Covid-19 status (Yi) without the vaccine (Di=0)

The treatment received determines which potential outcome we actually observe:

Yi=(1−Di)∗Yi(0)+Di∗Yi(1)

Potential outcomes are fixed, but we only observe one (of many) potential outcomes → Fundamental Problem of Causal Inference

Fundamental Problem of Causal Inference

The individual causal effect (ICE), τi, is defined as

τi≡Yi(1)−Yi(0)

  • The fundamental problem of causal inference is that we only ever see one potential outcome for an individual, and so it’s impossible to know the causal effect of some intervention for that individual

  • The ICE is unidentified

Causal Identification

Identification

  • Identification refers to what we can learn from the data available

  • A quantity of interest is identified if, with infinite data it can only take one value

  • For example, a coefficient in an equation can be unidentified if

    • We have more predictors than observations, or

    • Some of predictors are linear combinations of other predictors.

Causal Identification

  • Casual Identification refers to “the assumptions needed for statistical estimates to be given a causal interpretation” Keele (2015)

  • What’s Your Casual Identification Strategy What are the assumptions that make your research design credible?

  • Identification > Estimation

Observational vs Experimental Designs

  • Experimental designs are studies in which a causal variable of interest, the treatement, is manipulated by the researcher to examine its causal effects on some outcome of interest

  • Observational designs are studies in which a causal variable of interest is determined by someone/thing other than the researcher (nature, governments, people, etc.)

Causal Identification in Experimental Designs

The FPoCI is a problem of missing data

Recall that an individual causal effect τi, is defined as:

τi≡Yi(1)−Yi(0)

The problem is that for any one individual, we only observe Yi(1) or Yi(0), but never both.

  • If Paul got the vaccine (YPaul(Vaxxed)=Covid Free), then we don’t know what Paul’s health status would have been, had he not got the vaccine (YPaul(Unvaxxed)=???)

A statistical solution to the FPoCI

Rather than focus individual causal effects:

τi≡Yi(1)−Yi(0)

We focus on average causal effects (Average Treatment Effects [ATEs]):

E[τi]=E[Yi(1)−Yi(0)]⏞Average of a difference=E[Yi(1)]−E[Yi(0)]⏞Difference of Averages

When does the difference of averages provide us with a good estimate of the average difference?

Let’s consider a simple example

Does eating chocolate make you happy?

  • Yi happiness measured on a 0-10 scale

  • Di whether a person ate chocolate (D=1) or fruit (D=0)

  • Yi(1) a person’s happiness eating chocolate

  • Yi(0) a person’s happiness eating fruit

  • Xi a person’s self-reported preference (Xi∈ {chocolate, fruit })

Potential Outcomes:

Yi(1) Yi(0) τi
7 3 4
8 6 2
5 4 1
4 3 1
6 10 -4
8 9 -1
5 4 1
7 8 -1
4 3 1
6 0 6
E[Yi(1)] E[Yi(0)] E[τi]
6 5 1

  • If we could observe everyone’s potential outcomes, we could calculate the ICE

  • On average eating chocolate increases happiness by 1 point on our 10-point scale (ATE = 1)

  • Suppose we conducted a study and let folks select what they wanted to eat.

Potential Outcomes:

Yi(1) Yi(0) τi
7 3 4
8 6 2
5 4 1
4 3 1
6 10 -4
8 9 -1
5 4 1
7 8 -1
4 3 1
6 0 6
E[Yi(1)] E[Yi(0)] ATE
6 5 1

Observed Treatment:

xi di yi
chocolate 1 7
chocolate 1 8
chocolate 1 5
chocolate 1 4
fruit 0 10
fruit 0 9
chocolate 1 5
fruit 0 8
chocolate 1 4
chocolate 1 6
y¯d=1 y¯d=0 ATE^
5.57 9 -3.43

Observed Treatment:

xi di yi
chocolate 1 7
chocolate 1 8
chocolate 1 5
chocolate 1 4
fruit 0 10
fruit 0 9
chocolate 1 5
fruit 0 8
chocolate 1 4
chocolate 1 6
y¯d=1 y¯d=0 ATE^
5.57 9 -3.43

Selection Bias

  • Our estimate of the ATE is biased by the fact that folks who prefer fruit seem to be happier than folks who prefer chocolate in this example

  • In general, selection bias occurs when folks who receive the treatment differ systematically from folks who don’t

  • What if instead of letting people pick and choose, we randomly assigned half our respondents to chocolate and half to receive fruit

Potential Outcomes:

Yi(1) Yi(0) τi
7 3 4
8 6 2
5 4 1
4 3 1
6 10 -4
8 9 -1
5 4 1
7 8 -1
4 3 1
6 0 6
E[Yi(1)] E[Yi(0)] ATE
6 5 1

Randomly Assigned Treatment:

xi di yi
chocolate 1 7
chocolate 1 8
chocolate 0 4
chocolate 1 4
fruit 0 10
fruit 1 8
chocolate 0 4
fruit 0 8
chocolate 1 4
chocolate 0 0
y¯d=1 y¯d=0 ATE^
6.2 5.2 1

Randomly Assigned Treatment:

xi di yi
chocolate 1 7
chocolate 1 8
chocolate 0 4
chocolate 1 4
fruit 0 10
fruit 1 8
chocolate 0 4
fruit 0 8
chocolate 1 4
chocolate 0 0
y¯d=1 y¯d=0 ATE^
6.2 5.2 1

Random Assignment

  • When treatment has been randomly assigned, a difference in sample means provides an unbiased estimate of the ATE

  • The fact that our ATE^=ATE in this example is pure coincidence.

  • If we randomly assigned treatment a different way, we’d get a different estimate.

  • In general unbiased estimators will tend to be neither too high nor too low (e.g. E[θ^−θ]=0])

Estimating an Average Treatment Effect

If we treatment has been randomly assigned, we can estimate the ATE by taking the difference of means between treatment and control:

E[∑1mYim−∑m+1NYiN−m]=E[∑1mYim]⏞Average outcomeamong treatedunits−E[∑m+1NYiN−m]⏞Average outcomeamong controlunits=E[Yi(1)|Di=1]−E[Yi(0)|Di=0]

That is, the ATE is causally identified by the difference of means estimator in an experimental design

Random Assignment 1

xi di yi
chocolate 1 7
chocolate 1 8
chocolate 0 4
chocolate 1 4
fruit 0 10
fruit 1 8
chocolate 0 4
fruit 0 8
chocolate 1 4
chocolate 0 0
y¯d=1 y¯d=0 ATE^
6.2 5.2 1

Random Assignment 2

xi di yi
chocolate 0 3
chocolate 1 8
chocolate 0 4
chocolate 1 4
fruit 1 6
fruit 1 8
chocolate 0 4
fruit 1 7
chocolate 0 3
chocolate 0 0
y¯d=1 y¯d=0 ATE^
6.6 2.8 3.8

Random Assignment 3

xi di yi
chocolate 1 7
chocolate 0 6
chocolate 1 5
chocolate 1 4
fruit 0 10
fruit 0 9
chocolate 0 4
fruit 1 7
chocolate 1 4
chocolate 0 0
y¯d=1 y¯d=0 ATE^
5.4 5.8 -0.4

Distribution of Sample ATEs

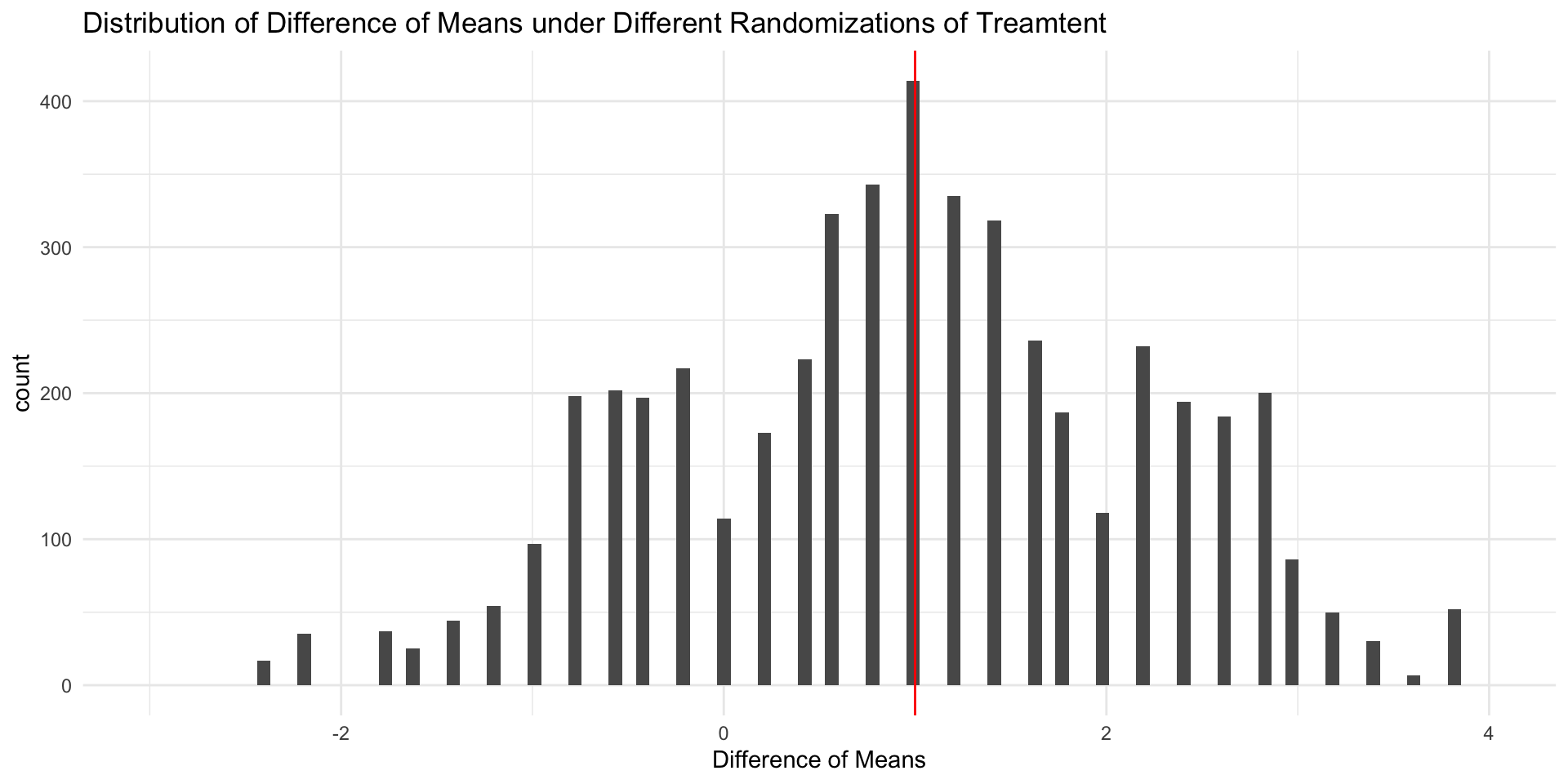
Why Random Assignment Matters?

Formally, randomly assigning treatments creates statistical independence ⫫(⫫) between treatment ( D ) and potential outcomes ( Y(1),Y(0) ) as well as any observed ( X ) or unobserved confounders ( U ):

⫫Yi(1),Yi(0),Xi,Ui⫫Di

Practically, what this means is that what we can observe ( differences in conditional means for treated and control ), provide good (unbiased) estimates of what we’re trying to learn about (Average Treatment Effects)

Causal Identification with Experimental Designs

Causal identification for experimental designs requires very few assumptions:

  • Independence (Satisfied by Randomization)

    • Y(1),Y(0),X,U,⊥D

  • SUTVA Stable Unit Treatment Value Assumption (Depends on features of the design)

    • No interference between units Yi(d1,d2,…,dN)=Yi(di)
    • No hidden values of the treatment/Variation in the treatment

Random assignment creates testable implications

  • If treatment has been randomly assigned, we would expect treatment and control groups to look similar in terms of pre-treatment covariates

    • We can show covariate balance by comparing the means in each treatment group

  • If the treatment had an effect, than we can credibly claim that that effect was due to the presence or absence of the treatment, and not some alternative explanation.

  • This type of clean apples-to-apples counterfactual comparison is what people mean when they talk about an experimental ideal

No Causation without Manipulation?

  • “No causation without manipulation” - Holland (1986)
  • Causal effects are well defined when we can imagine manipulating (changing) the value of Di and only Di
  • But what about the “effects” of things like:
    • Race
    • Sex
    • Democracy
  • Studying the effects of these factors requires strong theory and clever design Sen and Wasow (2016)

Estimating ATEs with the resume data

The Resume Experiment

Let’s take a look at the resume experiment from your text book and compare some of Imai’s code to its tidyverse equivalent

# make sure qss package is loaded
library(qss)
data("resume")

High level Overview (p. 34)

dim(resume)
[1] 4870    4
head(resume)
  firstname    sex  race call
1   Allison female white    0
2   Kristen female white    0
3   Lakisha female black    0
4   Latonya female black    0
5    Carrie female white    0
6       Jay   male white    0

High level Overview (p. 34)

summary(resume)
  firstname             sex                race                call        
 Length:4870        Length:4870        Length:4870        Min.   :0.00000  
 Class :character   Class :character   Class :character   1st Qu.:0.00000  
 Mode  :character   Mode  :character   Mode  :character   Median :0.00000  
                                                          Mean   :0.08049  
                                                          3rd Qu.:0.00000  
                                                          Max.   :1.00000

Crosstabs

race.call.tab <- table(race = resume$race,
                       call = resume$call)
race.call.tab
       call
race       0    1
  black 2278  157
  white 2200  235
addmargins(race.call.tab)
       call
race       0    1  Sum
  black 2278  157 2435
  white 2200  235 2435
  Sum   4478  392 4870

Tidy crosstab

resume %>%
  group_by(race, call)%>%
  summarise(
    n = n()
  )%>%
  pivot_wider(names_from = call, values_from = n)
# A tibble: 2 × 3
# Groups:   race [2]
  race    `0`   `1`
  <chr> <int> <int>
1 black  2278   157
2 white  2200   235

Calculating Call Back Rates

# Overall
sum(race.call.tab[,2])/nrow(resume)
[1] 0.08049281
# Black names
cb_bl <- sum(race.call.tab[1,2])/sum(race.call.tab[1,])
# White Names
cb_wh <- sum(race.call.tab[2,2])/sum(race.call.tab[2,])

# ATE
cb_wh - cb_bl
[1] 0.03203285

Calculating Call Back Rates with group_by()

resume %>%
  group_by(race)%>%
  summarise(
    call_back = mean(call)
  )
# A tibble: 2 × 2
  race  call_back
  <chr>     <dbl>
1 black    0.0645
2 white    0.0965

Factor variables in Base R

resume$type <- NA
resume$type[resume$race == "black" & resume$sex == "female"] <- "BlackFemale"
resume$type[resume$race == "black" & resume$sex == "male"] <- "BlackMale"
resume$type[resume$race == "white" & resume$sex == "female"] <- "WhiteFemale"
resume$type[resume$race == "white" & resume$sex == "male"] <- "WhiteMale"

Factor variables in Tidy R

resume %>%
  mutate(
    type_tidy = case_when(
      race == "black" & sex == "female" ~ "BlackFemale",
      race == "black" & sex == "male" ~ "BlackMale",
      race == "white" & sex == "female" ~ "WhiteFemale",
      race == "white" & sex == "male" ~ "WhiteMale"
    )
  ) -> resume

Comparing approaches

table(base= resume$type, tidy= resume$type_tidy)
             tidy
base          BlackFemale BlackMale WhiteFemale WhiteMale
  BlackFemale        1886         0           0         0
  BlackMale             0       549           0         0
  WhiteFemale           0         0        1860         0
  WhiteMale             0         0           0       575

Visualizing Call Back Rates by Name

  • Code
  • Figure
resume %>%
  group_by(race, sex,firstname)%>%
  summarize(
    Y = mean(call),
    n = n()
  )%>%
  arrange(desc(Y)) %>%
  mutate(
    firstname = forcats::fct_reorder(firstname,Y)
  )%>%
  ggplot(aes(Y, firstname,col=race, size=n))+
  geom_point() + 
  facet_grid(sex~.,scales = "free_y")

Broockman and Kalla (2016)

Reading Academic Papers

  • Reading academic papers is a skill and takes practice.
  • You should aim to answer the following:
    • What’s the research question?
    • What’s the theoretical framework?
    • What’s the empirical design?
    • What’s are the main results?

Study Design :A placebo-controlled field experiment

  1. Recruited from voter files to complete a baseline survey
  2. Among those who complete the survey, half are assigned to receive an intervention and half are assigned to receive a placebo
  3. Only some are actually home or open the door when the canvassers knock.
  4. These people are then recruited to participate in a series of surveys 3 days, 3 weeks, 6 weeks, and 3 months after the initial intervention.

Data for Thursday

Let’s load the data from the orginal study

load(url("https://pols1600.paultesta.org/files/data/03_lab.rda"))

Codebook

  • completed_baseline whether someone completed the baseline survey (“Survey”) or not (“No Survey”)
  • treatment_assigned what intervention someone who completed the baseline survey was assigned two (treatment= “Trans-Equality”, placebo = “Recycling”)
  • answered_door whether someone answered the door (“Yes”) or not (“No”) when a canvasser came to their door
  • treatment_group the treatment assignments of those who answered the door (treatment= “Trans-Equality”, placebo = “Recycling”)
  • vf_age the age of the person in years
  • vf_female the respondent’s sex (female = 1, male = 0)
  • vf_democrat whether the person was a registered Democract (Democrat=1, 0 otherwise)
  • vf_white whether the person was white (White=1, 0 otherwise)
  • vf_vg_12 whether the person voted in the 2012 general election (voted = 1, 0 otherwise)

HLO

glimpse(df)
Rows: 68,378
Columns: 14
$ completed_baseline <chr> "No Survey", "No Survey", "No Survey", "No Survey",…
$ treatment_assigned <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ answered_door      <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ treatment_group    <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ vf_age             <dbl> 23.00000, 38.00000, 48.00000, 49.20192, 49.20192, 4…
$ vf_female          <dbl> 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, …
$ vf_democrat        <dbl> 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, …
$ vf_white           <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, …
$ vf_vg_12           <dbl> 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, …
$ therm_trans_t0     <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t1     <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t2     <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t3     <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t4     <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…

Study Design

table(df$completed_baseline)

No Survey    Survey 
    66553      1825 
table(df$treatment_assigned)

     Recycling Trans-Equality 
           913            912 
table(df$answered_door)

  No  Yes 
1324  501 
table(df$treatment_group)

     Recycling Trans-Equality 
           255            246

Assessing balance in covariates

df %>%
  filter(completed_baseline == "Survey") %>%
  select(treatment_assigned,
         starts_with("vf_"))%>%
  group_by(treatment_assigned)%>%
  summarise(
    across(starts_with("vf_"), mean)
    ) -> pretreatment_balance

Assessing balance in covariates

pretreatment_balance
# A tibble: 2 × 6
  treatment_assigned vf_age vf_female vf_democrat vf_white vf_vg_12
  <chr>               <dbl>     <dbl>       <dbl>    <dbl>    <dbl>
1 Recycling            46.3     0.593       0.463    0.209    0.757
2 Trans-Equality       47.7     0.582       0.488    0.217    0.719

Assessing balance in covariates

  • Code
  • Balance
# Rearrange data
pretreatment_balance %>%
  # Pivot columns except treatement assigned
  pivot_longer(names_to = "covariate", values_to =  "value", -treatment_assigned) %>%
  # Pivot rows two two columns for treatment and placebo
  pivot_wider(names_from = treatment_assigned) %>%
  # Calculate covariate balance
  mutate(
    Difference = `Trans-Equality` - Recycling
  )
# A tibble: 5 × 4
  covariate   Recycling `Trans-Equality` Difference
  <chr>           <dbl>            <dbl>      <dbl>
1 vf_age         46.3             47.7      1.40   
2 vf_female       0.593            0.582   -0.0103 
3 vf_democrat     0.463            0.488    0.0246 
4 vf_white        0.209            0.217    0.00790
5 vf_vg_12        0.757            0.719   -0.0375

Summary

Summary

  • Causal Claims involve counterfactual comparisons

  • The fundamental problem of causal inference is that for an individual only observe one of many potential outcomes

  • Causal identification refers to the assumptions necessary to generate credible causal estimates

  • Identification for experimental designs follows from the random assignment of treatment which allows us to produce unbiased estimates of the Average Treatment Effect

References

Broockman, David, and Joshua Kalla. 2016. “Durably reducing transphobia: A field experiment on door-to-door canvassing.” Science 352 (6282): 220–24.

POLS 1600

1
POLS 1600 Causal Inference in Experimental Designs Updated Mar 3, 2025

  1. Slides

  2. Tools

  3. Close
  • POLS 1600
  • Overview
  • Class Plan
  • Annoucements
  • Group Assignments
  • Feedback
  • What did we like
  • What did we dislike
  • Setup
  • Setting your working directory when working “Live”
  • Packages for today
  • Review
  • Review: Data wrangling
  • Data transformations
  • Data Visualization
  • Practice
  • Practice
  • Causal Inference
  • Causal claims imply counterfactual comparisons
  • What’s the counterfactual for these claims:
  • Casual claims are all around us
  • Casual claims are all around us
  • Notation for Causal Inference
  • How to represent causal claims
  • General Notation: Variables
  • Expected Values
  • Conditional Expectations
  • Estimands, Estimators and Estimates
  • Error and Bias
  • Bias vs. variance
  • The bias-variance tradeoff
  • Potential outcomes notation
  • Fundamental Problem of Causal Inference
  • Causal Identification
  • Identification
  • Causal Identification
  • Observational vs Experimental Designs
  • Causal Identification in Experimental Designs
  • The FPoCI is a problem of missing data
  • A statistical solution to the FPoCI
  • Does eating chocolate make you happy?
  • Potential Outcomes:...
  • Potential Outcomes:...
  • Observed Treatment:...
  • Potential Outcomes:...
  • Randomly Assigned...
  • Estimating an Average Treatment Effect
  • Random Assignment...
  • Distribution of Sample ATEs
  • Why Random Assignment Matters?
  • Causal Identification with Experimental Designs
  • Random assignment creates testable implications
  • No Causation without Manipulation?
  • Estimating ATEs with the resume data
  • The Resume Experiment
  • High level Overview (p. 34)
  • High level Overview (p. 34)
  • Crosstabs
  • Tidy crosstab
  • Calculating Call Back Rates
  • Calculating Call Back Rates with group_by()
  • Factor variables in Base R
  • Factor variables in Tidy R
  • Comparing approaches
  • Visualizing Call Back Rates by Name
  • Broockman and Kalla (2016)
  • Reading Academic Papers
  • Study Design :A placebo-controlled field experiment
  • Data for Thursday
  • Codebook
  • HLO
  • Study Design
  • Assessing balance in covariates
  • Assessing balance in covariates
  • Assessing balance in covariates
  • Summary
  • Summary
  • References
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • ? Keyboard Help