POLS 1600
Causal Inference in
Experimental Designs
Updated Apr 22, 2025
Overview
Class Plan
- Announcements
- Feedback
- Review
- Class plan
- Causal Inference
- Notation for Causal Inference
- Causal Identification
- Causal Identification in Experiments
resumedata from QSS (Skipping, but their for your reference)- Explore Broockman and Kalla (2016)
Annoucements
We start taking attendance this week
Readings for this week:
- QSS Chapter 2: pp. 38–65
- Broockman and Kalla (2016)
No class next Tuesdays
No lab next Thursday
Meet your groups!
Group Assignments
Feedback
What did we like
What did we dislike
Setup
Every time you work in R
Save your file to your course or project folder
Set your working directory to where your file is saved
Load, and if needed, install packages
Maybe change some global options in your .Qmd file
Setting your working directory when working “Live”
Packages for today
## Pacakges for today
the_packages <- c(
## R Markdown
"kableExtra","DT",
## Tidyverse
"tidyverse", "lubridate", "forcats",
"haven", "labelled",
## Extensions for ggplot
"ggmap","ggrepel", "ggridges",
"ggthemes", "ggpubr", "GGally",
"scales", "dagitty", "ggdag", #<<
# Data
"COVID19","maps","mapdata",
"qss" #<<
)
## Define a function to load (and if needed install) packages
ipak <- function(pkg){
new.pkg <- pkg[!(pkg %in% installed.packages()[, "Package"])]
if (length(new.pkg))
install.packages(new.pkg, dependencies = TRUE)
sapply(pkg, require, character.only = TRUE)
}
## Install (if needed) and load libraries in the_packages
ipak(the_packages)kableExtra DT tidyverse lubridate forcats haven labelled
TRUE TRUE TRUE TRUE TRUE TRUE TRUE
ggmap ggrepel ggridges ggthemes ggpubr GGally scales
TRUE TRUE TRUE TRUE TRUE TRUE TRUE
dagitty ggdag COVID19 maps mapdata qss
TRUE TRUE TRUE TRUE TRUE TRUE Review
Review: Data wrangling
Data transformations
You want to:
Load some data
Combine multiple functions
Look at your data
Recode your data
Transform your data
You could use
read_*functions%>%the “pipe” operatorglimpse()head(),filter(),select(),arrange()mutate(),case_when(),ifelse()summarize(),group_by()
Data Visualization
The grammar of graphics
At minimum you need:
dataaestheticmappingsgeometries
Hey Jude, take a sad plot and make it better by:
labelsthemesstatisticscooridnatesfacets- transforming your data before plotting
Practice
- Create two variables
xandyxshould be a random variable with 100 observations from a random normal (rnorm) distribution with mean 0 and standard deviation 1yshould be a function of x plus the square of a random normal distribution with mean 0 and standard deviation 1
- Combine
xandyinto adata.framecalleddf summarizethemean,median, standard deviation (sd), 16th and 84th percentile (quantile) ofxandyand save this to an object calleddf_sum- Plot the distributions of
xandy, separately, using a density plot (geom_density)- Add a rug to each density plot
- Add vertical lines for the mean and median of each variable
- A vertical lines at the 16th and and 84th percentile of each plot
- Hint use your object
df_sumas the data for these geometries
- Hint use your object
Practice
- Create two variables
xandyxshould be a random variable with 100 observations from a random normal (rnorm) distribution with mean 0 and standard deviation 1yshould be a function of x plus the square of a random normal distribution with mean 0 and standard deviation 1
- Combine
xandyinto adata.framecalleddf summarizethemean,median, standard deviation (sd), 16th and 84th percentile (quantile) ofxandyand save this to an object calleddf_sum- Plot the distributions of
xandy, separately, using a density plot (geom_density)- Add a rug to each density plot
- Add vertical lines for the mean and median of each variable
- A vertical lines at the 16th and and 84th percentile of each plot
- Hint: use your object
df_sumas the data for these geometries
- Hint: use your object
# Load libraries
library(tidyverse)
# Set seed for reproducibility
set.seed(123)
# Number of observations
n <- 1000
# Generate data
x <- rnorm(n, mean = 0, sd = 1)
y <- x + (rnorm(n, mean = 0, sd = 1))^2
# Create dataframe
df <- data.frame(x = x, y = y)
# Calculate summary statistics
df_sum <- df %>%
dplyr::summarise(
x_mean = mean(x),
x_median = median(x),
x_sd = sd(x),
x_16th = quantile(x, probs = .16),
x_84th = quantile(x, probs = .84),
y_mean = mean(y),
y_median = median(y),
y_sd = sd(y),
y_16th = quantile(y, probs = .16),
y_84th = quantile(y, probs = .84)
)
df_sum x_mean x_median x_sd x_16th x_84th y_mean y_median
1 0.01612787 0.009209639 0.991695 -1.01607 0.9869428 1.036354 0.7302196
y_sd y_16th y_84th
1 1.738673 -0.3879478 2.390059fig_x <- df %>%
ggplot(aes(x))+
geom_density()+
geom_rug()+
geom_vline(
data = df_sum,
aes(xintercept = x_mean, col="Mean"))+
geom_vline(
data = df_sum,
aes(xintercept = x_median, col="Median"),
linetype = "dashed")+
geom_vline(
data = df_sum,
aes(xintercept = x_16th, col="16th percentile"))+
geom_vline(
data = df_sum,
aes(xintercept = x_84th, col="84th percentile"))+
geom_segment(
aes(y=.45, yend=.45,
x = df_sum$x_mean - df_sum$x_sd,
xend = df_sum$x_mean + df_sum$x_sd)
)+
ylim(0,.5)+
labs(
col = "Statistic"
)
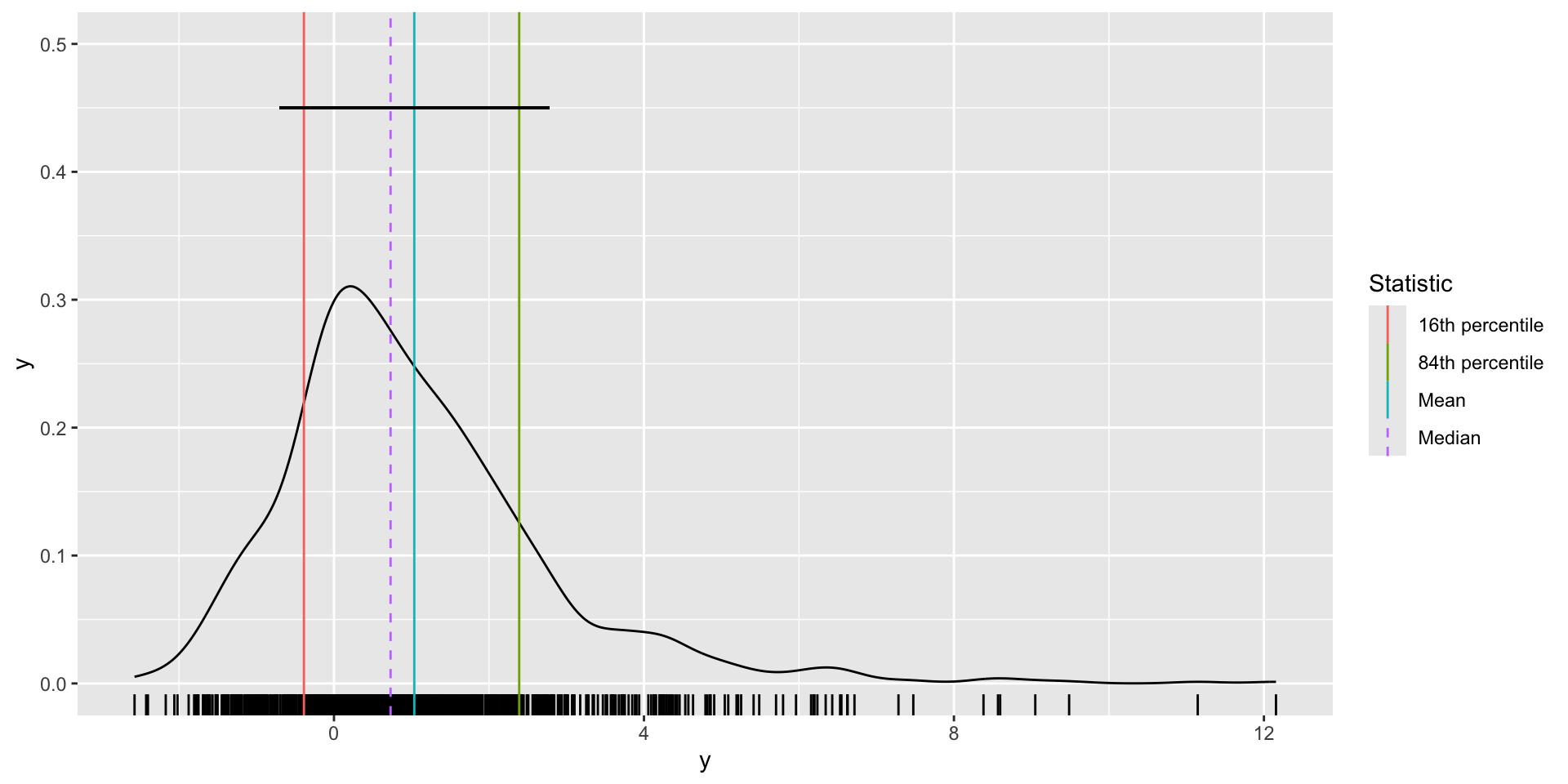
fig_y <- df %>%
ggplot(aes(y))+
geom_density()+
geom_rug()+
geom_vline(
data = df_sum,
aes(xintercept = y_mean, col="Mean"))+
geom_vline(
data = df_sum,
aes(xintercept = y_median, col="Median"),
linetype = "dashed")+
geom_vline(
data = df_sum,
aes(xintercept = y_16th, col="16th percentile"))+
geom_vline(
data = df_sum,
aes(xintercept = y_84th, col="84th percentile"))+
geom_segment(
aes(y=.45, yend=.45,
x = df_sum$y_mean - df_sum$y_sd,
xend = df_sum$y_mean + df_sum$y_sd)
)+
ylim(0,.5)+
labs(
col = "Statistic"
)
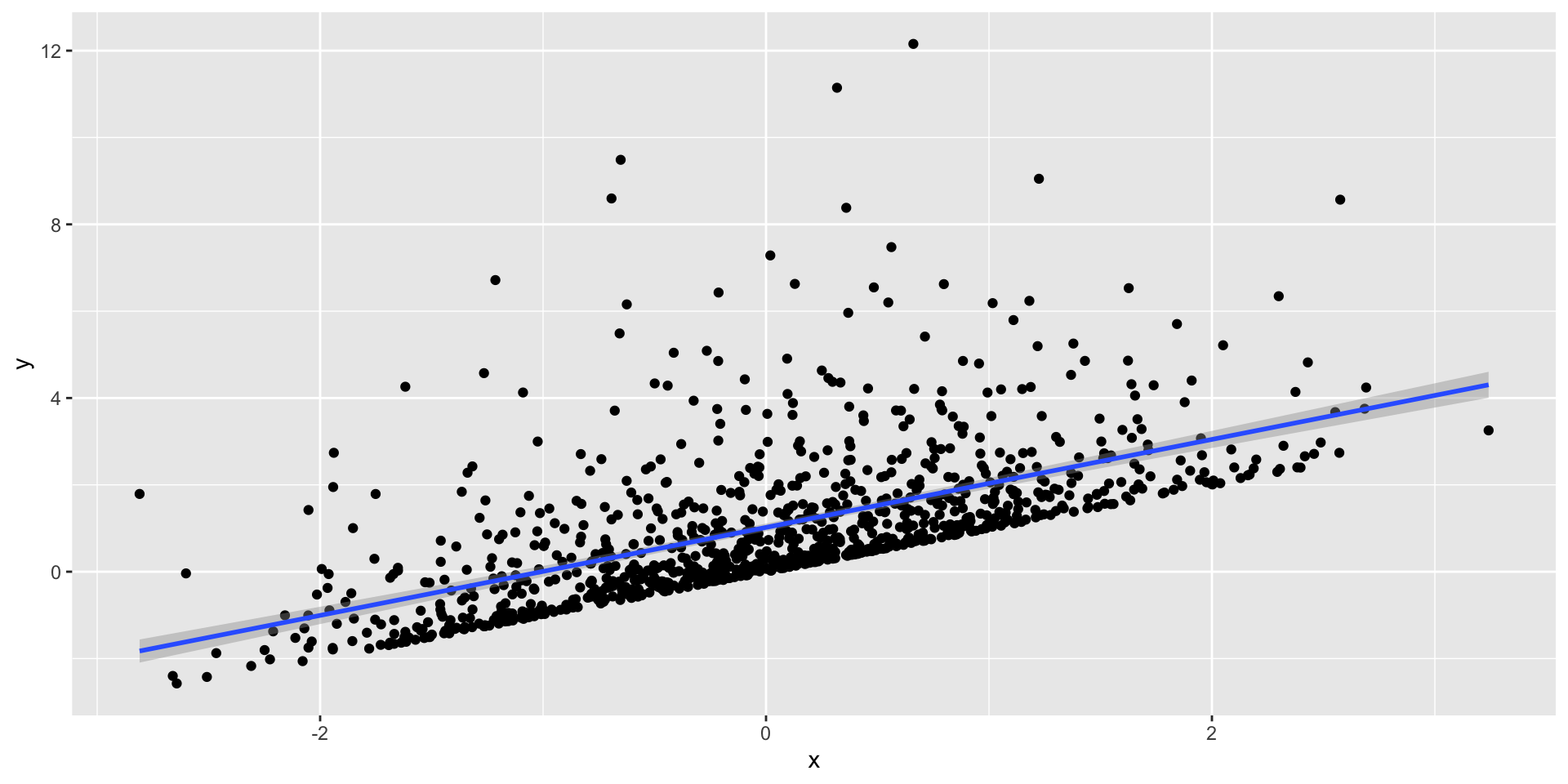
cor(df$x, df$y)[1] 0.5779469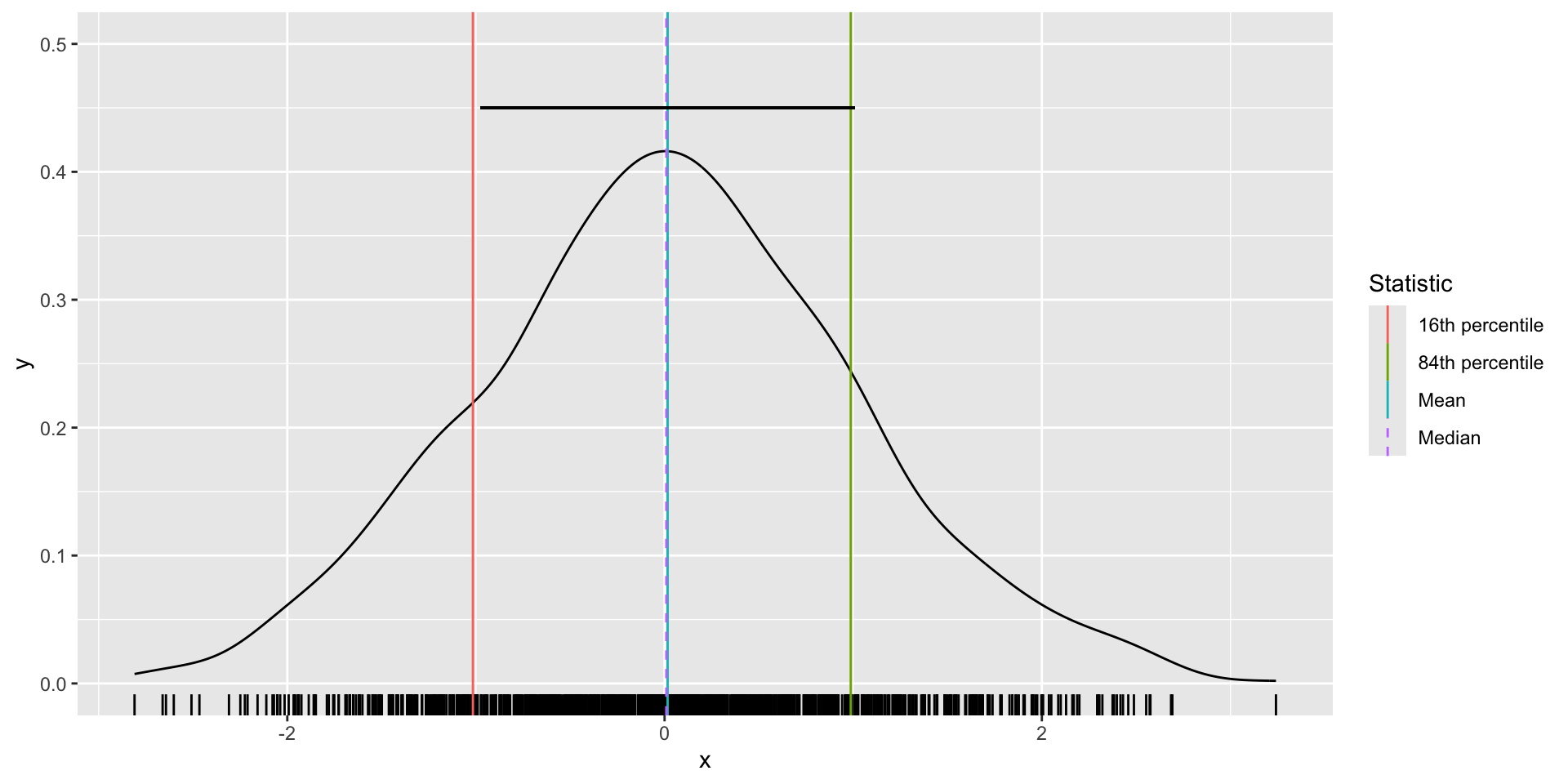
Measures of central tendency describe what’s typical
Measures of dispersion describe variation around what’s typical
Causal Inference
Causal claims imply counterfactual comparisons
Causal claims imply counterfactual comparisons
What would have happened if we were to change some aspect of the world?

What’s the counterfactual for these claims:
Foreign aid increases develop
Joe Rogan cost Kamala the 2024 election
Democracies don’t fight wars with other democracies
Universal Pre-K improves child development
Casual claims are all around us


Casual claims are all around us
What are some questions that interest you?
What are the counterfactual comparisons they imply?
Notation for Causal Inference
How to represent causal claims
In this course, we will use two forms of notation to describe our causal claims.
Directed Acyclic Graphs (DAGs, next lecture)
Potential Outcomes Notation
General Notation: Variables
Your outcome of interestDan indicator of treatment statusD=1D=0
Zan of assignment statusZ=1Z=0
Xa covariate or predictor we can measure/observeUunmeasured covariates
Expected Values
The
Conditional Expectations
The
Estimands, Estimators and Estimates
Estimand the thing we want to know.
- Sometimes called a parameter (
- The expected value of heights in POLS 1600 (
- Sometimes called a parameter (
Estimator a rule or method for calculating an estimate of our estimand
- An average of a sample of 10 student’s heights in POLS 1600
Estimate: a value produced by our estimator for some data
- The average of our 10 person sample is
5'10''
- The average of our 10 person sample is
Error and Bias
Formally, we’ll say an estimate,
Bias or error,
An estimator is unbiased if, on average, the errors equal 0
Bias vs. variance
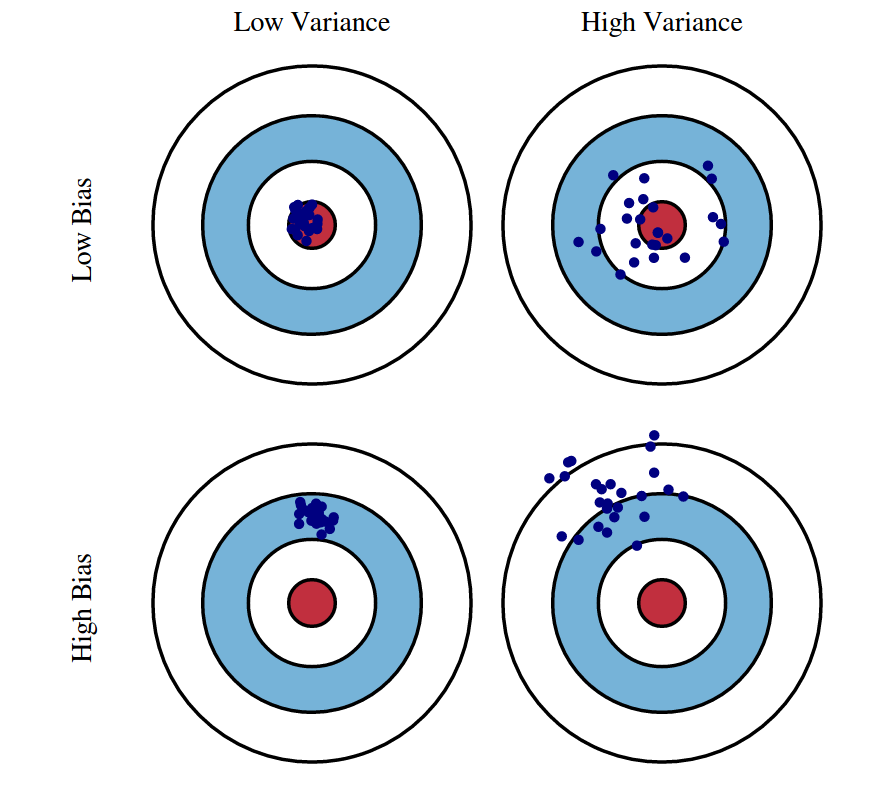
The bias-variance tradeoff
Potential outcomes notation
- Shorthand for
- Paul’s Covid-19 status (
- Shorthand for
- Shorthand for
- Paul’s Covid-19 status (
- Shorthand for
The treatment received determines which potential outcome we actually observe:
Potential outcomes are fixed, but we only observe one (of many) potential outcomes
Fundamental Problem of Causal Inference
The individual causal effect (ICE),
The fundamental problem of causal inference is that we only ever see one potential outcome for an individual, and so it’s impossible to know the causal effect of some intervention for that individual
The ICE is unidentified
Causal Identification
Identification
Identification refers to what we can learn from the data available
A quantity of interest is identified if, with infinite data it can only take one value
For example, a coefficient in an equation can be unidentified if
We have more predictors than observations, or
Some of predictors are linear combinations of other predictors.
Causal Identification
Casual Identification refers to “the assumptions needed for statistical estimates to be given a causal interpretation” Keele (2015)
What’s Your Casual Identification Strategy What are the assumptions that make your research design credible?
Identification > Estimation
Observational vs Experimental Designs
Experimental designs are studies in which a causal variable of interest, the treatement, is manipulated by the researcher to examine its causal effects on some outcome of interest
Observational designs are studies in which a causal variable of interest is determined by someone/thing other than the researcher (nature, governments, people, etc.)
Causal Identification in Experimental Designs
The FPoCI is a problem of missing data
Recall that an individual causal effect
The problem is that for any one individual, we only observe
- If Paul got the vaccine
A statistical solution to the FPoCI
Rather than focus individual causal effects:
We focus on average causal effects (Average Treatment Effects [ATEs]):
When does the difference of averages provide us with a good estimate of the average difference?
Let’s consider a simple example
Does eating chocolate make you happy?
Potential Outcomes:
| 7 | 3 | 4 |
| 8 | 6 | 2 |
| 5 | 4 | 1 |
| 4 | 3 | 1 |
| 6 | 10 | -4 |
| 8 | 9 | -1 |
| 5 | 4 | 1 |
| 7 | 8 | -1 |
| 4 | 3 | 1 |
| 6 | 0 | 6 |
| 6 | 5 | 1 |
If we could observe everyone’s potential outcomes, we could calculate the ICE
On average eating chocolate increases happiness by 1 point on our 10-point scale (ATE = 1)
Suppose we conducted a study and let folks select what they wanted to eat.
Potential Outcomes:
| 7 | 3 | 4 |
| 8 | 6 | 2 |
| 5 | 4 | 1 |
| 4 | 3 | 1 |
| 6 | 10 | -4 |
| 8 | 9 | -1 |
| 5 | 4 | 1 |
| 7 | 8 | -1 |
| 4 | 3 | 1 |
| 6 | 0 | 6 |
| 6 | 5 | 1 |
Observed Treatment:
| chocolate | 1 | 7 |
| chocolate | 1 | 8 |
| chocolate | 1 | 5 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 0 | 9 |
| chocolate | 1 | 5 |
| fruit | 0 | 8 |
| chocolate | 1 | 4 |
| chocolate | 1 | 6 |
| 5.57 | 9 | -3.43 |
Observed Treatment:
| chocolate | 1 | 7 |
| chocolate | 1 | 8 |
| chocolate | 1 | 5 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 0 | 9 |
| chocolate | 1 | 5 |
| fruit | 0 | 8 |
| chocolate | 1 | 4 |
| chocolate | 1 | 6 |
| 5.57 | 9 | -3.43 |
Selection Bias
Our estimate of the ATE is biased by the fact that folks who prefer fruit seem to be happier than folks who prefer chocolate in this example
In general, selection bias occurs when folks who receive the treatment differ systematically from folks who don’t
What if instead of letting people pick and choose, we randomly assigned half our respondents to chocolate and half to receive fruit
Potential Outcomes:
| 7 | 3 | 4 |
| 8 | 6 | 2 |
| 5 | 4 | 1 |
| 4 | 3 | 1 |
| 6 | 10 | -4 |
| 8 | 9 | -1 |
| 5 | 4 | 1 |
| 7 | 8 | -1 |
| 4 | 3 | 1 |
| 6 | 0 | 6 |
| 6 | 5 | 1 |
Randomly Assigned Treatment:
| chocolate | 1 | 7 |
| chocolate | 1 | 8 |
| chocolate | 0 | 4 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 1 | 8 |
| chocolate | 0 | 4 |
| fruit | 0 | 8 |
| chocolate | 1 | 4 |
| chocolate | 0 | 0 |
| 6.2 | 5.2 | 1 |
Randomly Assigned Treatment:
| chocolate | 1 | 7 |
| chocolate | 1 | 8 |
| chocolate | 0 | 4 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 1 | 8 |
| chocolate | 0 | 4 |
| fruit | 0 | 8 |
| chocolate | 1 | 4 |
| chocolate | 0 | 0 |
| 6.2 | 5.2 | 1 |
Random Assignment
When treatment has been randomly assigned, a difference in sample means provides an unbiased estimate of the ATE
The fact that our
If we randomly assigned treatment a different way, we’d get a different estimate.
In general unbiased estimators will tend to be neither too high nor too low (e.g.
Estimating an Average Treatment Effect
If we treatment has been randomly assigned, we can estimate the ATE by taking the difference of means between treatment and control:
That is, the ATE is causally identified by the difference of means estimator in an experimental design
Random Assignment 1
| chocolate | 1 | 7 |
| chocolate | 1 | 8 |
| chocolate | 0 | 4 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 1 | 8 |
| chocolate | 0 | 4 |
| fruit | 0 | 8 |
| chocolate | 1 | 4 |
| chocolate | 0 | 0 |
| 6.2 | 5.2 | 1 |
Random Assignment 2
| chocolate | 0 | 3 |
| chocolate | 1 | 8 |
| chocolate | 0 | 4 |
| chocolate | 1 | 4 |
| fruit | 1 | 6 |
| fruit | 1 | 8 |
| chocolate | 0 | 4 |
| fruit | 1 | 7 |
| chocolate | 0 | 3 |
| chocolate | 0 | 0 |
| 6.6 | 2.8 | 3.8 |
Random Assignment 3
| chocolate | 1 | 7 |
| chocolate | 0 | 6 |
| chocolate | 1 | 5 |
| chocolate | 1 | 4 |
| fruit | 0 | 10 |
| fruit | 0 | 9 |
| chocolate | 0 | 4 |
| fruit | 1 | 7 |
| chocolate | 1 | 4 |
| chocolate | 0 | 0 |
| 5.4 | 5.8 | -0.4 |
Distribution of Sample ATEs
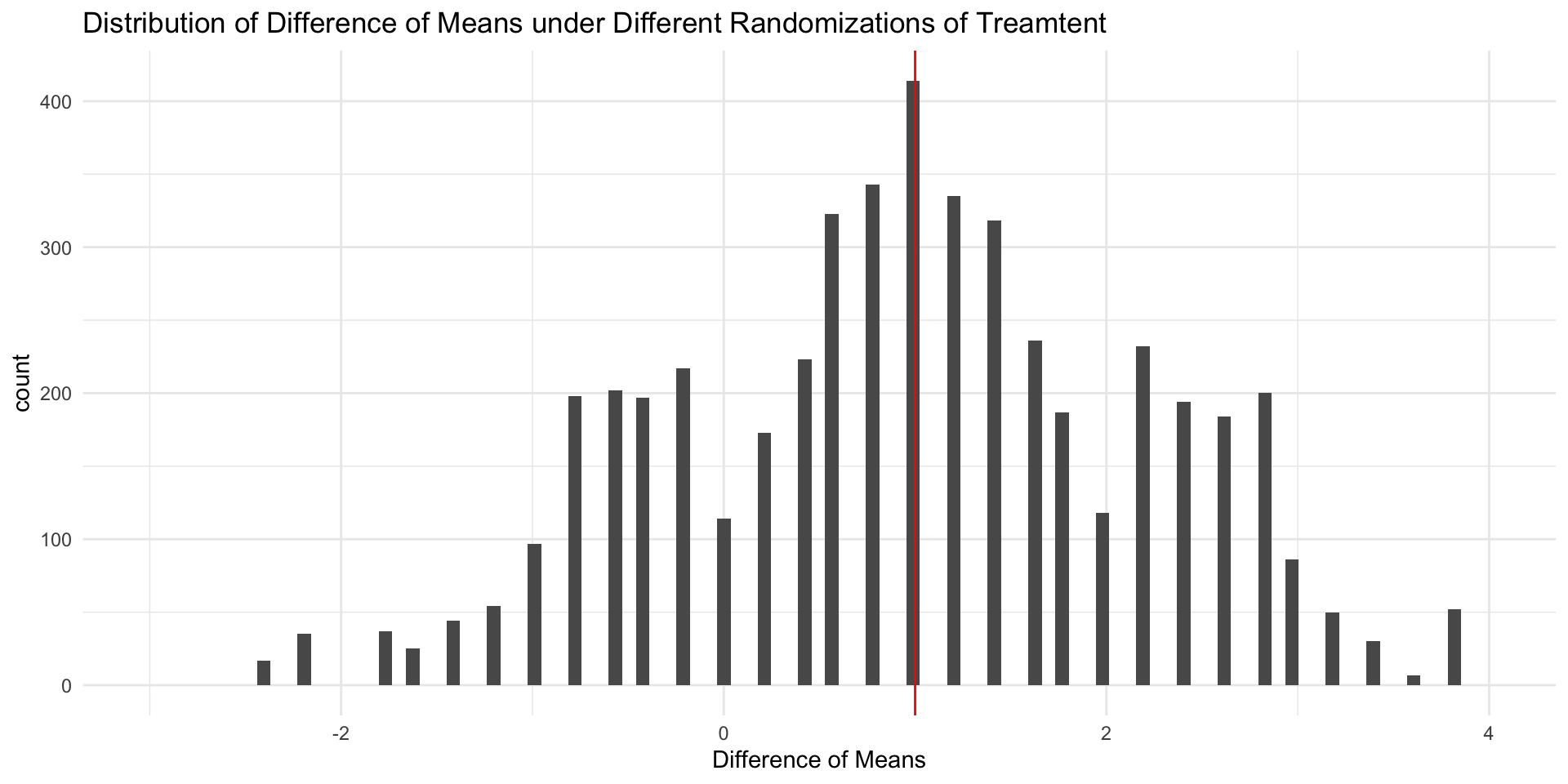
Why Random Assignment Matters?
Formally, randomly assigning treatments creates statistical independence
Practically, what this means is that what we can observe ( differences in conditional means for treated and control ), provide good (unbiased) estimates of what we’re trying to learn about (Average Treatment Effects)
Causal Identification with Experimental Designs
Causal identification for experimental designs requires very few assumptions:
Independence (Satisfied by Randomization)
SUTVA Stable Unit Treatment Value Assumption (Depends on features of the design)
- No interference between units
- No hidden values of the treatment/Variation in the treatment
- No interference between units
Random assignment creates testable implications
If treatment has been randomly assigned, we would expect treatment and control groups to look similar in terms of pre-treatment covariates
- We can show covariate balance by comparing the means in each treatment group
If the treatment had an effect, than we can credibly claim that that effect was due to the presence or absence of the treatment, and not some alternative explanation.
This type of clean apples-to-apples counterfactual comparison is what people mean when they talk about an experimental ideal
No Causation without Manipulation?
- “No causation without manipulation” - Holland (1986)
- Causal effects are well defined when we can imagine manipulating (changing) the value of
- But what about the “effects” of things like:
- Race
- Sex
- Democracy
- Studying the effects of these factors requires strong theory and clever design Sen and Wasow (2016)
Estimating ATEs with the resume data
The Resume Experiment
Let’s take a look at the resume experiment from your text book and compare some of Imai’s code to its tidyverse equivalent
High level Overview (p. 34)
High level Overview (p. 34)
Crosstabs
Tidy crosstab
Calculating Call Back Rates
Calculating Call Back Rates with group_by()
Factor variables in Base R
resume$type <- NA
resume$type[resume$race == "black" & resume$sex == "female"] <- "BlackFemale"
resume$type[resume$race == "black" & resume$sex == "male"] <- "BlackMale"
resume$type[resume$race == "white" & resume$sex == "female"] <- "WhiteFemale"
resume$type[resume$race == "white" & resume$sex == "male"] <- "WhiteMale"Factor variables in Tidy R
Comparing approaches
Visualizing Call Back Rates by Name
Broockman and Kalla (2016)
Reading Academic Papers
- Reading academic papers is a skill and takes practice.
- You should aim to answer the following:
- What’s the research question?
- What’s the theoretical framework?
- What’s the empirical design?
- What’s are the main results?
Study Design :A placebo-controlled field experiment
- Recruited from voter files to complete a baseline survey
- Among those who complete the survey, half are assigned to receive an intervention and half are assigned to receive a placebo
- Only some are actually home or open the door when the canvassers knock.
- These people are then recruited to participate in a series of surveys 3 days, 3 weeks, 6 weeks, and 3 months after the initial intervention.
Data for Thursday
Let’s load the data from the orginal study
Codebook
completed_baselinewhether someone completed the baseline survey (“Survey”) or not (“No Survey”)treatment_assignedwhat intervention someone who completed the baseline survey was assigned two (treatment= “Trans-Equality”, placebo = “Recycling”)answered_doorwhether someone answered the door (“Yes”) or not (“No”) when a canvasser came to their doortreatment_groupthe treatment assignments of those who answered the door (treatment= “Trans-Equality”, placebo = “Recycling”)vf_agethe age of the person in yearsvf_femalethe respondent’s sex (female = 1, male = 0)vf_democratwhether the person was a registered Democract (Democrat=1, 0 otherwise)vf_whitewhether the person was white (White=1, 0 otherwise)vf_vg_12whether the person voted in the 2012 general election (voted = 1, 0 otherwise)
HLO
Rows: 68,378
Columns: 14
$ completed_baseline <chr> "No Survey", "No Survey", "No Survey", "No Survey",…
$ treatment_assigned <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ answered_door <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ treatment_group <chr> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ vf_age <dbl> 23.00000, 38.00000, 48.00000, 49.20192, 49.20192, 4…
$ vf_female <dbl> 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, …
$ vf_democrat <dbl> 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, …
$ vf_white <dbl> 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, …
$ vf_vg_12 <dbl> 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, …
$ therm_trans_t0 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t1 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t2 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t3 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…
$ therm_trans_t4 <int> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,…Study Design
Assessing balance in covariates
Assessing balance in covariates
Assessing balance in covariates
# Rearrange data
pretreatment_balance %>%
# Pivot columns except treatement assigned
pivot_longer(names_to = "covariate", values_to = "value", -treatment_assigned) %>%
# Pivot rows two two columns for treatment and placebo
pivot_wider(names_from = treatment_assigned) %>%
# Calculate covariate balance
mutate(
Difference = `Trans-Equality` - Recycling
)# A tibble: 5 × 4
covariate Recycling `Trans-Equality` Difference
<chr> <dbl> <dbl> <dbl>
1 vf_age 46.3 47.7 1.40
2 vf_female 0.593 0.582 -0.0103
3 vf_democrat 0.463 0.488 0.0246
4 vf_white 0.209 0.217 0.00790
5 vf_vg_12 0.757 0.719 -0.0375 Summary
Summary
Causal Claims involve counterfactual comparisons
The fundamental problem of causal inference is that for an individual only observe one of many potential outcomes
Causal identification refers to the assumptions necessary to generate credible causal estimates
Identification for experimental designs follows from the random assignment of treatment which allows us to produce unbiased estimates of the Average Treatment Effect
References

POLS 1600
