POLS 1600

Casual Inference in
Observational Designs &
Simple Linear Regression

Updated May 31, 2024

Overview

Overview

  • Announcements
  • Setup
  • Feedback
  • Review
  • Class plan

Learing goals

  • Introduce the concept of Directed Acyclic Graphs to describe causal relationships and illustrate potential bias from confounders and colliders

  • Discuss three approaches to covariate adjustment

    • Subclassification
    • Matching
    • Linear Regression

  • Begin discussing three research designs to make causal claims with observational data

    • Differences-in-Differences (If there’s time)
    • Regression Discontinuity Designs
    • Instrumental Variables

Annoucements

  • Sit with your groups (for now)

  • Updated timeline for final projects next week

Group Assignments

Feedback

What did we like

What did we dislike

Grinding an Iron Pestle into a Needle

Me

  • Less is more
  • Go slow
  • Provide labs/code earlier
  • Adapt assignments/policies

You

  • Active reading
  • Do tutorials
  • Review labs before class
  • Review comments after class
  • Ask for help
  • Don’t give up!

Review

Review

  • Data wrangling

  • Descriptive Statistics

  • Levels of understanding

  • Data visualization

Data Wrangling

Data wrangling

You're learning how to map conceptual tasks to commands in R
Skill Common Commands
Setup R library(), ipak()
Load data read_csv(), load()
Get HLO of data df$x, glimpse(), table(), summary()
Transform data <-, mutate(), ifelse(), case_when()
Reshape data pivot_longer(), left_join()
Summarize data numerically mean(), median(), summarise(), group_by()
Summarize data graphically ggplot(), aes(), geom_

Mapping Concepts to Code

  • Takes time and practice

  • Don’t be afraid to FAAFO

  • Don’t worry about memorizing everything.

  • Statistical programming is necessary to actually do empirical research

  • Learning to code will help us understand statistical concepts.

  • Learning to think programmatically and algorithmically will help us tackle complex problems

Descriptive Statiscs

Descriptive statistics

Levels of understanding

Levels of understanding in POLS 1600

  • Conceptual

  • Practical

  • Definitional

  • Theoretical

Let’s illustrate these different levels of understanding about our old friend the mean

Mean: Conceptual Understanding

A mean is:

  • A common and important measure of central tendency (what’s typical)

  • It’s the arithmetic average you learned in school

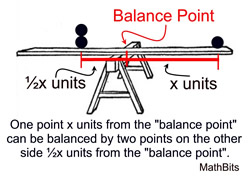
  • We can think of it as the balancing point of a distribution

  • A conditional mean is the average of one variable \(X\), when some other variable, \(Z\) takes a value \(z\)

    • Think about the average height in our class (unconditional mean) vs the average height among men and women ([conditional means].{blue})

Mean as a balancing point

Source

Mean: Practical

There are lots of ways to calculate means in R

  • The simplest is to use the mean() function

    • If our data have missing values, we need to to tell R to remove them
mean(df$x, na.rm=T)

Conditional Means: Practical

  • To calculate a conditional mean we could us a logical index [df$z == 1]
mean(df$x[df$z == 1], na.rm=T)
  • If we wanted to a calculate a lot of conditional means we could use the mean() in combination with group_by() and summarise()
df %>% 
  group_by(z)%>%
  summarise(
    x = mean(x, na.rm=T)
  )

Mean: Definitional

Formally, we define the arithmetic mean of \(x\) as \(\bar{x}\):

\[ \bar{x} = \frac{1}{n}\left (\sum_{i=1}^n{x_i}\right ) = \frac{x_1+x_2+\cdots +x_n}{n} \]

In words, this formula says, to calculate the average of x, we sum up all the values of \(x_i\) from observation \(i=1\) to \(i=n\) and then divide by the total number of observations \(n\)

Mean: Definitional

  • In this class, I don’t put a lot of weight on memorizing definitions (that’s what Google’s for).

  • But being comfortable with “the math” is important and useful

  • Definitional knowledge is a prerequisite for understanding more theoretical claims.

Mean: Theoretical

Suppose I asked you to show that the sum of deviations from a mean equals 0?

\[ \text{Claim:} \sum_{i=1}^n (x_i -\bar{x}) = 0 \]

Mean: Theoretical

Knowing the definition of an arithmetic mean, we could write:

\[ \begin{aligned} \sum_{i=1}^n (x_i -\bar{x}) &= \sum_{i=1}^n x_i - \sum_{i=1}^n\bar{x} & \text{Distribute Summation}\\ &= \sum_{i=1}^n x_i - n\bar{x} & \text{Summing a constant, } \bar{x}\\ &= \sum_{i=1}^n x_i - n\times \left ( \frac{1}{n} \sum_{i=1}^n{x_i}\right ) & \text{Definition of } \bar{x}\\ &= \sum_{i=1}^n x_i - \sum_{i=1}^n{x_i} & n \times \frac{1}{n}=1\\ &= 0 \end{aligned} \]

Mean: Theoretical

Why do we care?

  • Showing the deviations sum to 0 is another way of saying the mean is a balancing point.

  • This turns out to be a useful property of means that will reappear throughout the course

  • If I asked you to make a prediction, \(\hat{x}\) of a random person’s height in this class, the mean would have the lowest mean squared error (MSE \(=\frac{1}{n}\sum (x_i - \hat{x_i})^2)\)

Mean: Theoretical

Occasionally, you’ll read or here me say say things like:

The sample mean is an unbiased estimator of the population mean

In a statistics class, we would take time to prove this.

The sample mean is an unbiased estimator of the population mean

Claim:

Let \(x_1, x_2, \dots x_n\) from a random sample from a population with mean \(\mu\) and variance \(\sigma^2\)

Then:

\[ \bar{x} = \frac{1}{n}\left (\sum_{i=1}^n x_i\right ) \]

is an unbiased estimator of \(\mu\)

\[ E[\bar{x}] = \mu \]

The sample mean is an unbiased estimator of the population mean

Proof:

\[ \begin{aligned} E\left [\bar{x} \right] &= E\left [\frac{1}{n}\left (\sum_{i=1}^n x_i \right) \right] & \text{Definition of } \bar{x} \\ &= \frac{1}{n} \sum_{i=1}^nE\left [ x_i \right] & \text{Linearity of Expectations} \\ &= \frac{1}{n} \sum_{i=1}^n \mu & E[x_i] = \mu \\ &= \frac{n}{n} \mu & \sum_{i=1}^n \mu = n\mu \\ &= \mu & \blacksquare \\ \end{aligned} \]

Levels of understanding

In this course, we tend to emphasize the

  • Conceptual

  • Practical

Over

  • Definitional

  • Theoretical

In an intro statistics class, the ordering might be reversed.

Trade offs:

  • Pro: We actually get to work with data and do empirical research much sooner
  • Cons: We substitute intuitive understandings for more rigorous proofs

Data Visualization

Data Visualization

  • The grammar of graphics

  • At minimum you need:

    • data
    • aesthetic mappings
    • geometries

  • Take a sad plot and make it better by:

    • labels
    • themes
    • statistics
    • cooridnates
    • facets
    • transforming your data before plotting

You are about to be reincarnated: HLO

df$reincarnation
<labelled<double>[10]>: You're about to be re-incarnated. Do you want to come back as a:
 [1] 1 1 1 7 6 1 6 6 7 1

Labels:
 value                  label
     1    Animal/land dweller
     6       Bird/air dweller
     7     Fish/water dweller
     2                 Insect
     9                  Plant
    10 Single-celled organism
table(df$reincarnation)

1 6 7 
5 3 2

Basic Plot

df %>%
  ggplot(aes(x = reincarnation, 
             fill = reincarnation))+
  geom_bar(
    stat = "count"
  )

Use a factor to label and order responses

df %>%
  mutate(
    # Turn numeric values into factor labels 
    Reincarnation = forcats::as_factor(reincarnation),
    # Order factor in decreasing frequency of levels
    Reincarnation = forcats::fct_infreq(Reincarnation),
    # Reverse order so levels are increasing in frequency
    Reincarnation = forcats::fct_rev(Reincarnation),
    # Rename explanations
    Why = reincarnation_why
  ) -> df
table(recode= df$Reincarnation, original = df$reincarnation)
                        original
recode                   1 6 7
  Single-celled organism 0 0 0
  Plant                  0 0 0
  Insect                 0 0 0
  Fish/water dweller     0 0 2
  Bird/air dweller       0 3 0
  Animal/land dweller    5 0 0

Revised figure

df %>% # Data
  # Aesthetics
  ggplot(aes(x = Reincarnation, 
             fill = Reincarnation))+
  # Geometry
  geom_bar(stat = "count")+ # Statistic
  ## Include levels of Reincarnation w/ no values
  scale_x_discrete(drop=FALSE)+
  # Don't include a legend
  scale_fill_discrete(drop=FALSE, guide="none")+
  # Flip x and y
  coord_flip()+
  # Remove lines
  theme_classic() -> fig1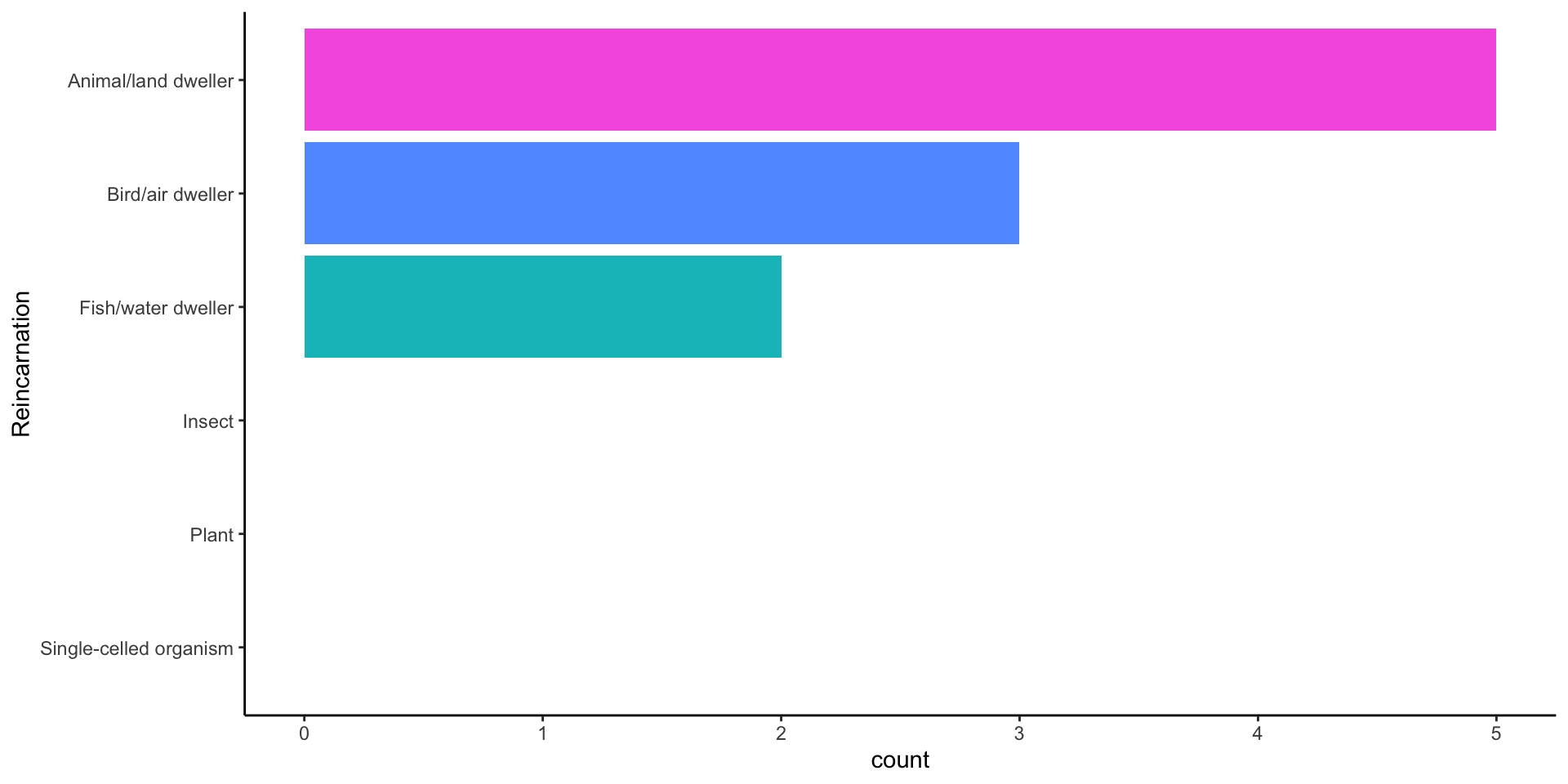

What creature and why?

Adding labelled values

df %>%
  mutate(
    # Create numeric id
    id = 1:n(),
    # Create a label with 3 answers and NA elsewhere
    Label = case_when(
      id == 10 ~ str_wrap(reincarnation_why[10],30),
      id == 4 ~ str_wrap(reincarnation_why[4],30),
      id == 7 ~ str_wrap(reincarnation_why[7],30),
      TRUE ~ NA_character_

    )

  ) -> df
# Calculate totals before calling ggplot
plot_df <- df %>%
  group_by(Reincarnation)%>% 
  summarise( 
    Count = n(), 
    Why = na.omit(unique(Label)) 
  )

You’re about to be reincarnated:

plot_df %>%
  ggplot(aes(x = Reincarnation, 
             y = Count,
             fill = Reincarnation, 
             label=Why))+
  geom_bar(stat = "identity")+ #<<
  ## Include levels of Reincarnation w/ no values
  scale_x_discrete(drop=FALSE)+
  # Don't include a legend
  scale_fill_discrete(drop=FALSE, guide="none")+
  coord_flip()+
  labs(x = "",y="",title="You're about to be reincarnated.\nWhat do you want to come back as?")+
  theme_classic()+
  ggrepel::geom_label_repel(
    fill="white",
    nudge_y = 1, 
    hjust = "left",
    size=3,
    arrow = arrow(length = unit(0.015, "npc"))
    )+ 
  scale_y_continuous(
    breaks = c(0,2,4,6,8,10,12),
    expand = expansion(add =c(0,6))
    ) -> fig1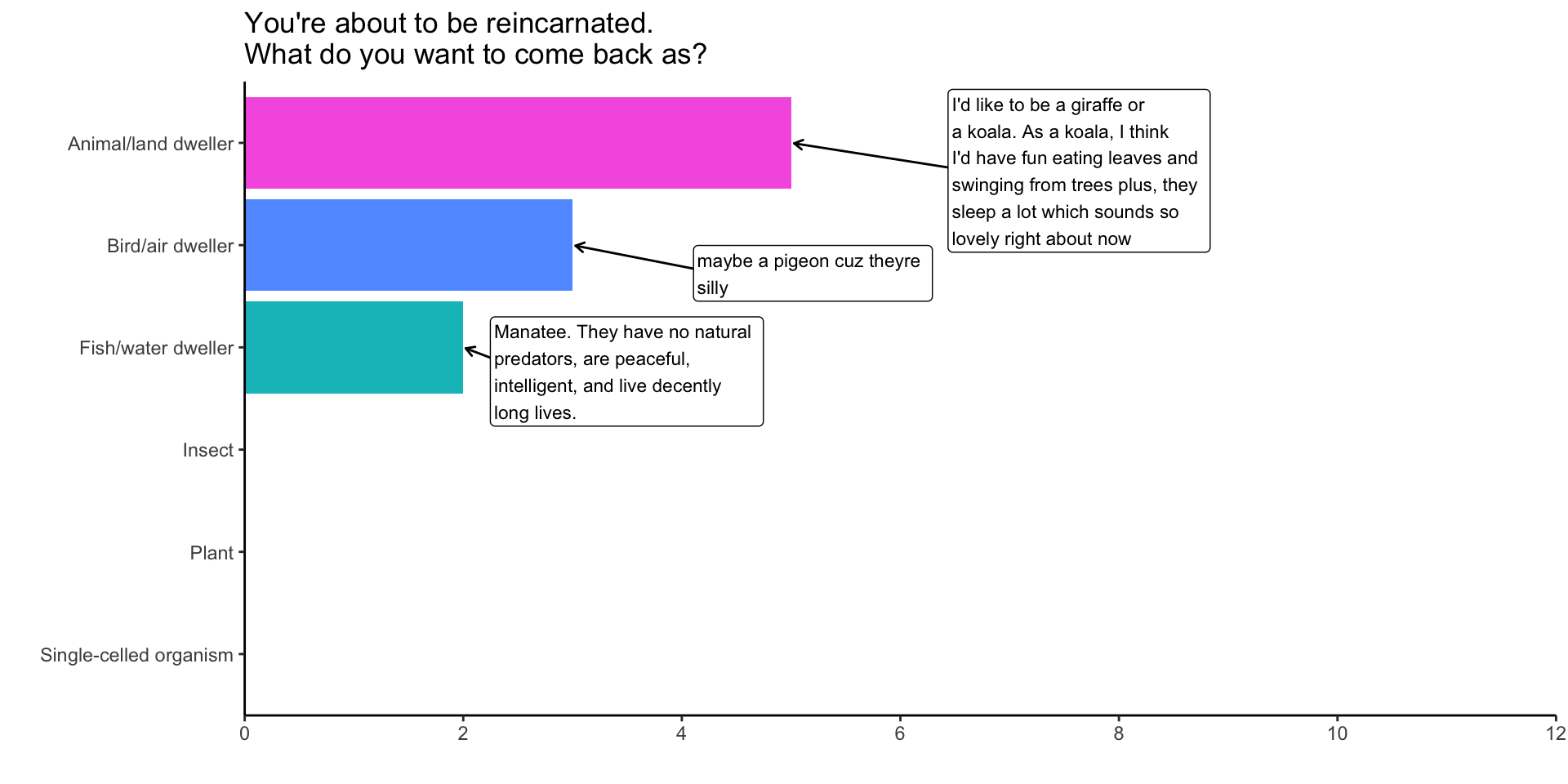

Data visualization is an iterative process

  • Data visualization is an iterative process

  • Good data viz requires lots of data transformations

  • Start with a minimum working example and build from there

  • Don’t let the perfect be the enemy of the good enough.

Setup

New packages

This week’s lab we’ll be using the dataverse package to download data on presidential elections

Next week’s lab, we’ll be using the tidycensus package to download census data.

We’ll also need to install a census API to get the data.

Here’s a detailed guide of what we’ll do in class right now.

Install new packages

These packages are easier to install live:

install.packages("dataverse")
install.packages("tidycensus")
install.packages("easystats")
install.packages("DeclareDesign")

Census API

Please follow these steps so you can download data directly from the U.S. Census here:

  1. Install the tidycensus package
  2. Load the installed package
  3. Request an API key from the Census
  4. Check your email
  5. Activate your key
  6. Install your API key in R
  7. Check that everything worked

Packages for today

## Pacakges for today
the_packages <- c(
  ## R Markdown
  "kableExtra","DT","texreg",
  ## Tidyverse
  "tidyverse", "lubridate", "forcats", "haven", "labelled",
  ## Extensions for ggplot
  "ggmap","ggrepel", "ggridges", "ggthemes", "ggpubr", 
  "GGally", "scales", "dagitty", "ggdag", "ggforce",
  # Data 
  "COVID19","maps","mapdata","qss","tidycensus", "dataverse", 
  # Analysis
  "DeclareDesign", "easystats", "zoo"
)

## Define a function to load (and if needed install) packages

#| label = "ipak"
ipak <- function(pkg){
    new.pkg <- pkg[!(pkg %in% installed.packages()[, "Package"])]
    if (length(new.pkg)) 
        install.packages(new.pkg, dependencies = TRUE)
    sapply(pkg, require, character.only = TRUE)
}

## Install (if needed) and load libraries in the_packages
ipak(the_packages)
   kableExtra            DT        texreg     tidyverse     lubridate 
         TRUE          TRUE          TRUE          TRUE          TRUE 
      forcats         haven      labelled         ggmap       ggrepel 
         TRUE          TRUE          TRUE          TRUE          TRUE 
     ggridges      ggthemes        ggpubr        GGally        scales 
         TRUE          TRUE          TRUE          TRUE          TRUE 
      dagitty         ggdag       ggforce       COVID19          maps 
         TRUE          TRUE          TRUE          TRUE          TRUE 
      mapdata           qss    tidycensus     dataverse DeclareDesign 
         TRUE          TRUE          TRUE          TRUE          TRUE 
    easystats           zoo 
         TRUE          TRUE

Previewing the Lab

Red Covid

Red Covid New York Times, 27 September, 2021

Red Covid, an Update New York Times, 18 February, 2022

Preview of the Lab

Please download Thursday’s lab here

  • Conceptually, this lab is designed to help reinforce the relationship between linear models like \(y=\beta_0 + \beta_1x\) and the conditional expectation function \(E[Y|X]\).

  • Substantively, we will explore whether David Leonhardt’s claims about Red Covid the political polarization of vaccines and its consequences

Lab: Questions 1-5: Review

Questions 1-5 are designed to reinforce your data wrangling skills. In particular, you will get practice:

  • Creating and recoding variables using mutate()
  • Calculating a moving average or rolling mean using the rollmean() function from the zoo package
  • Transforming the data on presidential elections so that it can be merged with the data on Covid-19 using the pivot_wider() function.
  • Merging data together using the left_join() function.

Lab: Questions 6-10: Simple Linear Regression

  • In question 6, you will see how calculating conditional means provides a simple test of “Red Covid” claim.

  • In question 7, you will see how a linear model returns the same information as these conditional means (in a sligthly different format)

  • In question 8, you will get practice interpreting linear models with continuous predictors (i.e. predictors that take on a range of values)

  • In question 9, you will get practice visualizing these models and using the figures help interpret your results substantively.

  • Question 10 asks you to play the role of a skeptic and consider what other factors might explain the relationships we found in Questions 6-9. We will explore these factors in next week’s lab.

Before Thursday

The following slides provide detailed explanations of all the code you’ll need for each question.

  • Please run this code before class on Thursday

  • We will review this material together at the start of class, but you will spend most of our time on the Questions 6-10

Q1: Setup your workspace

Q1 asks you to setup your workspace

This means loading and, if needed, installing the packages you will use.

## Pacakges for today
the_packages <- c(
  ## R Markdown
  "kableExtra","DT","texreg",
  ## Tidyverse
  "tidyverse", "lubridate", "forcats", "haven", "labelled",
  ## Extensions for ggplot
  "ggmap","ggrepel", "ggridges", "ggthemes", "ggpubr", 
  "GGally", "scales", "dagitty", "ggdag", "ggforce",
  # Data 
  "COVID19","maps","mapdata","qss","tidycensus", "dataverse", 
  # Analysis
  "DeclareDesign", "easystats", "zoo"
)

## Define a function to load (and if needed install) packages

#| label = "ipak"
ipak <- function(pkg){
    new.pkg <- pkg[!(pkg %in% installed.packages()[, "Package"])]
    if (length(new.pkg)) 
        install.packages(new.pkg, dependencies = TRUE)
    sapply(pkg, require, character.only = TRUE)
}

## Install (if needed) and load libraries in the_packages
ipak(the_packages)

Q2 Load the data

To explore Leonhardt’s claims about Red Covid, we’ll need data on:

  • Covid-19
  • The 2020 Presidential Election

Q2.1 Load the Covid-19 Data

To load data on Covid-19 just run this

load(url("https://pols1600.paultesta.org/files/data/covid.rda"))

Q2.2 Load Election Data

Q2.2. asks you to write code that will download data presidential elections from 1976 to 2020 from the MIT Election Lab’s dataverse

  • Once you’ve installed the dataverse package you should be able to do this:
# Try this code first
Sys.setenv("DATAVERSE_SERVER" = "dataverse.harvard.edu")

pres_df <- dataverse::get_dataframe_by_name(
  "1976-2020-president.tab",
  "doi:10.7910/DVN/42MVDX"
)

# If the code above fails, comment out and uncomment the code below:

# load(url("https://pols1600.paultesta.org/files/data/pres_df.rda"))

Q3 Describe the structure of each dataset

Question 3 asks you to describe the structure of each dataset.

  • Specifically, it asks you to get a high level overview of covid and pres_df and describe the unit of analysis in each dataset:
    • Describe substantively what specific, observation each row in the dataset corresponds to
    • In covid covid dataset, the unit of analysis is a state-date

Q3 Describe the structure of each dataset

Here’s some possible code you could use to get a quick HLO of each dataset:

# check names in `covid`
names(covid)

# take a quick look values of each variable

glimpse(covid)

# Look at first few observations for:
# date, administrative_area_level_2, 

covid %>% 
  select(date, administrative_area_level_2) %>%
  head()

# Summarize data to get a better sense of the unit of observastion

covid %>% 
  group_by(administrative_area_level_2) %>%
  summarise(
    n = n(), # Number of observations for each state
    start_date = min(date, na.rm = T),
    end_date = max(date, na.rm=T)
  ) -> hlo_covid_df

hlo_covid_df


# How many unique values of date and state are their:

n_dates <- length(unique(covid$date))
n_states <- length(unique(covid$administrative_area_level_2))
n_dates
n_states

# If we had observations for every state on every date then the number of rows 
# in the data 
dim(covid)[1]
# Should equal
dim(covid)[1] == n_dates * n_states

# This is what economists would call an unbalanced panel
# check names in `pres_df`
names(pres_df)

# take a quick look values of each variable

glimpse(pres_df)

# Unit of analysis is a year-state-candidate
pres_df %>% 
  select(year, state_po, candidate) %>%
  head()

# How many states?
length(unique(pres_df$state_po))



# How many candidates and parties on the ballot in a given election year
pres_df %>% 
  group_by(year) %>%
  summarise(
    n_candidates = length(unique(candidate)),
    # Look at both party_detailed and party_simplified
    n_parties_detailed = length(unique(party_detailed)),
    n_parties_simplified = length(unique(party_simplified))
  ) -> hlo_pres_df
hlo_pres_df

# Look at 2020
# pres_df$candidate[pres_df$year == "2020"]

Q4 Recode the data for analysis

Using our understanding of the structure of the data, Q4 asks you to:

  • Recode the Covid-19 data like we’ve done before plus
  • Calculate rolling means, 7 and 14 day averages
  • Reshape, recode, and filter the presidential election data

Q4.1 Recode the Covid-19

This is the same code we’ve used before to create covid_us from covid with the addition of code to calculate a rolling mean or moving average of the number of new cases

# Create a vector containing of US territories
territories <- c(
  "American Samoa",
  "Guam",
  "Northern Mariana Islands",
  "Puerto Rico",
  "Virgin Islands"
  )

# Filter out Territories and create state variable
covid_us <- covid %>%
  filter(!administrative_area_level_2 %in% territories)%>%
  mutate(
    state = administrative_area_level_2
  )

# Calculate new cases, new cases per capita, and 7-day average

covid_us %>%
  dplyr::group_by(state) %>%
  mutate(
    new_cases = confirmed - lag(confirmed),
    new_cases_pc = new_cases / population *100000,
    new_cases_pc_7da = zoo::rollmean(new_cases_pc, 
                                     k = 7, 
                                     align = "right",
                                     fill=NA )
    ) -> covid_us

# Recode facemask policy

covid_us %>%
mutate(
  # Recode facial_coverings to create face_masks
    face_masks = case_when(
      facial_coverings == 0 ~ "No policy",
      abs(facial_coverings) == 1 ~ "Recommended",
      abs(facial_coverings) == 2 ~ "Some requirements",
      abs(facial_coverings) == 3 ~ "Required shared places",
      abs(facial_coverings) == 4 ~ "Required all times",
    ),
    # Turn face_masks into a factor with ordered policy levels
    face_masks = factor(face_masks,
      levels = c("No policy","Recommended",
                 "Some requirements",
                 "Required shared places",
                 "Required all times")
    ) 
    ) -> covid_us

# Create year-month and percent vaccinated variables

covid_us %>%
  mutate(
    year = year(date),
    month = month(date),
    year_month = paste(year, 
                       str_pad(month, width = 2, pad=0), 
                       sep = "-"),
    percent_vaccinated = people_fully_vaccinated/population*100  
    ) -> covid_us
# Calculate new cases, new cases per capita, and 7-day average

covid_us %>%
  dplyr::group_by(state) %>%
  mutate(
    new_cases = confirmed - lag(confirmed),
    new_cases_pc = new_cases / population *100000,
    new_cases_pc_7day = zoo::rollmean(new_cases_pc, 
                                     k = 7, 
                                     align = "right",
                                     fill=NA )
    ) -> covid_us

Q4.2 Calculate Rolling Means of Covid Deaths

Q4.2 asks you to create new measures of the 7-day and 14-day averages of new deaths from Covid-19 per 100,000 residents

It encourages you to use the code new_cases_pc_7da as a template

To build your coding skills, try writing this yourself, then comparing it to the code in the next tab:

covid_us %>%
  dplyr::group_by(state) %>%
  mutate(
    new_deaths = deaths - lag(deaths),
    new_deaths_pc = new_deaths / population *100000,
    new_deaths_pc_7day = zoo::rollmean(new_deaths_pc, 
                                     k = 7, 
                                     align = "right",
                                     fill=NA ),
    new_deaths_pc_14day = zoo::rollmean(new_deaths_pc, 
                                     k = 14, 
                                     align = "right",
                                     fill=NA )
    ) -> covid_us

Rolling Averages

The next slides aren’t necessary for the lab but are designed to illustrate:

  • the concept of a rolling mean
  • what the code does
  • why might prefer rolling averages over daily values

Look at the output of zoo::rollmean()

covid_us %>%
  filter(date > "2020-03-05") %>%
  select(date,new_cases_pc,new_cases_pc_7day)
# A tibble: 52,580 × 4
# Groups:   state [51]
   state     date       new_cases_pc new_cases_pc_7day
   <chr>     <date>            <dbl>             <dbl>
 1 Minnesota 2020-03-06      NA                NA     
 2 Minnesota 2020-03-07       0                NA     
 3 Minnesota 2020-03-08       0.0177           NA     
 4 Minnesota 2020-03-09       0                NA     
 5 Minnesota 2020-03-10       0.0177           NA     
 6 Minnesota 2020-03-11       0.0355           NA     
 7 Minnesota 2020-03-12       0.0709           NA     
 8 Minnesota 2020-03-13       0.0887            0.0329
 9 Minnesota 2020-03-14       0.124             0.0507
10 Minnesota 2020-03-15       0.248             0.0836
# ℹ 52,570 more rows

Comparing Daily Cases to Rolling Average

The following code illustrates how a 7-day rolling mean smooths (new_cases_pc_7da) over the noisiness of the daily measure

covid_us %>%
  filter(date > "2020-03-05", 
         state == "Minnesota") %>%
  select(date,
         new_cases_pc,
         new_cases_pc_7day)%>%
  ggplot(aes(date,new_cases_pc ))+
  geom_line(aes(col="Daily"))+
  # set y aesthetic for second line of rolling average
  geom_line(aes(y = new_cases_pc_7day,
                col = "7-day average")
            ) +
  theme(legend.position="bottom")+
    labs( col = "Measure",
    y = "New Cases Per 100k", x = "",
    title = "Minnesota"
  ) -> fig_covid_mn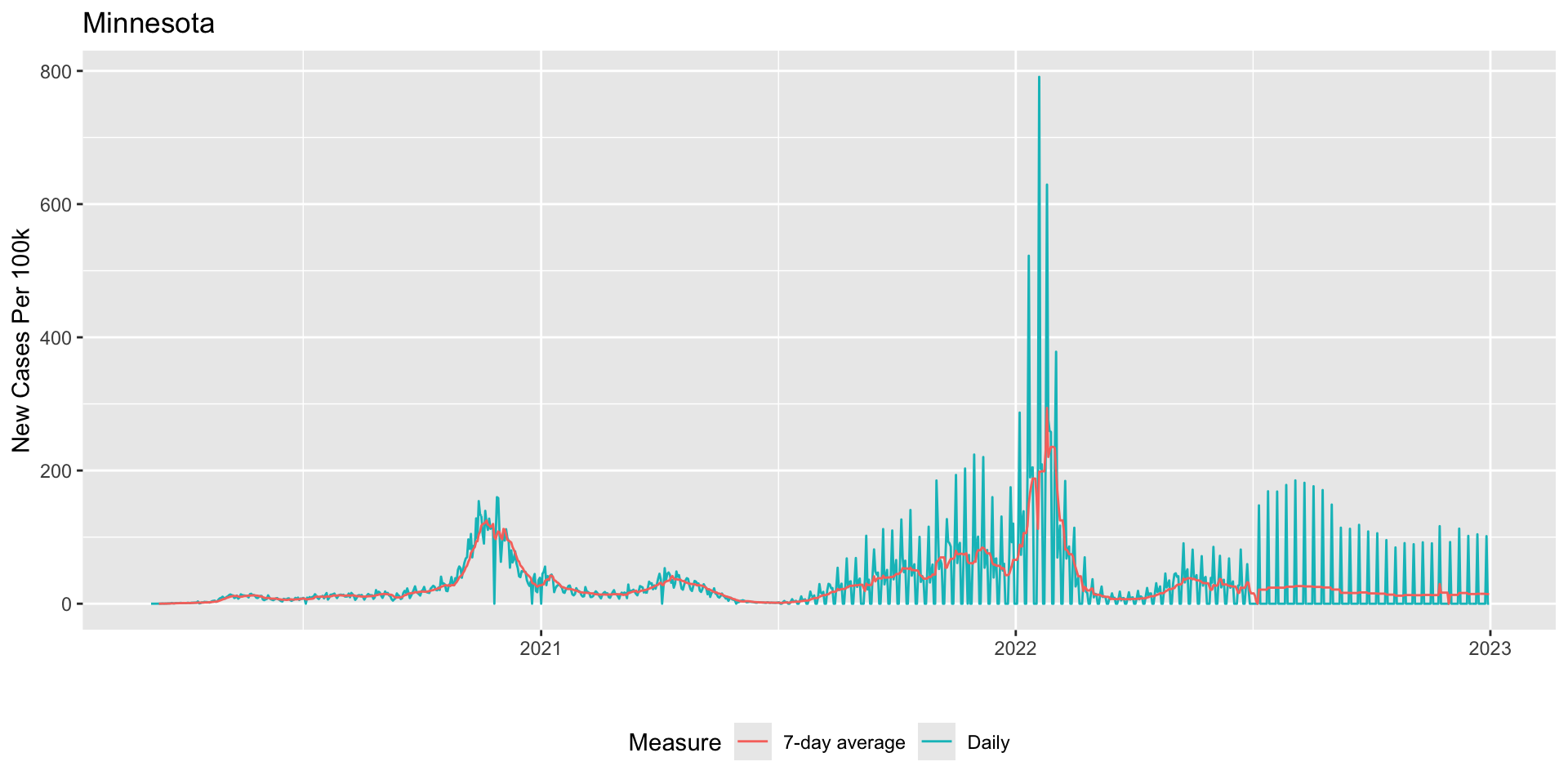

Q4.3 Recode Presidential data

Q4.3 Gives you a long list of steps to recode, reshape, and filter pres_df to produce pres_df2020

Most of this is review but it can seem like a lot.

Walk through the provided code and see if you can map each conceptual step in Q4.3 to its implementation in the code

pres_df %>%
  mutate(
    year_election = year,
    state = str_to_title(state),
    # Fix DC
    state = ifelse(state == "District Of Columbia", "District of Columbia", state)
  ) %>%
  filter(party_simplified %in% c("DEMOCRAT","REPUBLICAN"))%>%
  filter(year == 2020) %>%
  select(state, state_po, year_election, party_simplified, candidatevotes, totalvotes
         ) %>%
  pivot_wider(names_from = party_simplified,
              values_from = candidatevotes) %>%
  mutate(
    dem_voteshare = DEMOCRAT/totalvotes *100,
    rep_voteshare = REPUBLICAN/totalvotes*100,
    winner = forcats::fct_rev(factor(ifelse(rep_voteshare > dem_voteshare,"Trump","Biden")))
  ) -> pres2020_df

# Check Output:

glimpse(pres2020_df)
Rows: 51
Columns: 9
$ state         <chr> "Alabama", "Alaska", "Arizona", "Arkansas", "California"…
$ state_po      <chr> "AL", "AK", "AZ", "AR", "CA", "CO", "CT", "DE", "DC", "F…
$ year_election <dbl> 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 2020, 20…
$ totalvotes    <dbl> 2323282, 359530, 3387326, 1219069, 17500881, 3279980, 18…
$ DEMOCRAT      <dbl> 849624, 153778, 1672143, 423932, 11110250, 1804352, 1080…
$ REPUBLICAN    <dbl> 1441170, 189951, 1661686, 760647, 6006429, 1364607, 7147…
$ dem_voteshare <dbl> 36.56999, 42.77195, 49.36469, 34.77506, 63.48395, 55.011…
$ rep_voteshare <dbl> 62.031643, 52.833143, 49.055981, 62.395730, 34.320724, 4…
$ winner        <fct> Trump, Trump, Biden, Trump, Biden, Biden, Biden, Biden, …

Q5 merging data

Q5 asks you to merge the 2020 election data from pres2020_df into covid_us using the common state variable in each dataset using the function left_join()

dim(covid_us)
[1] 53678    61
dim(pres2020_df)
[1] 51  9
covid_us <- covid_us %>% left_join(
  pres2020_df,
  by = c("state" = "state")
)
dim(covid_us) 
[1] 53678    69

Advice for merging

When merging datasets:

  • Check the matches in your joining variables
    • Make sure the values state are the same in each dataset
    • Check for differences in spelling, punctuation, etc.
  • Check the dimensions of output of your left_join()
    • If there is a 1-1 match the number of rows should be the same before after
# Should be 51 states and DC in each
sum(unique(pres_df$state) %in% covid_us$state)
[1] 0
# Look at each state variable
## With [] index
pres_df$state[1:5]
[1] "ALABAMA" "ALABAMA" "ALABAMA" "ALABAMA" "ALABAMA"
covid_us$state[1:5]
[1] "Minnesota" "Minnesota" "Minnesota" "Minnesota" "Minnesota"
# Matching is case sensitive 

# make pres_df$state title case

## Base R:
pres_df$state <- str_to_title(pres_df$state )
## Tidy R:
pres_df %>% 
  mutate(
    state = str_to_title(state )
  ) -> pres_df

# Should be 51
sum(unique(pres_df$state) %in% covid_us$state)
[1] 50
# Find the mismatch:
unique(pres_df$state[!pres_df$state %in% covid_us$state])
[1] "District Of Columbia"
# Two equivalent ways to fix this mismatch
## Base R: Quick fix to change spelling of DC
pres_df$state[pres2020_df$state == "District Of Columbia"] <- "District of Columbia"

## Tidy R: Quick fix to change spelling of DC

pres_df %>% 
  mutate(
    state = ifelse(test = state == "District Of Columbia",
                   yes = "District of Columbia",
                   no = state
                   )
  ) -> pres_df


# Problem Solved
sum(unique(pres2020_df$state) %in% covid_us$state)
[1] 51

Causal Inference

Causal inference is about counterfactual comparisons

  • Causal inference is about counterfactual comparisons

    • What would have happened if some aspect of the world either had or had not been present

Causal Identification

  • Casual Identification refers to “the assumptions needed for statistical estimates to be given a causal interpretation” Keele (2015)]

    • What do we need to assume to make our claims about cause and effect credible

  • Experimental Designs rely on randomization of treatment to justify their causal claims

  • Observational Designs require additional assumptions and knowledge to make causal claims

Experimental Designs

  • Experimental designs are studies in which a causal variable of interest, the treatement, is manipulated by the researcher to examine its causal effects on some outcome of interest

  • Random assignment is the key to causal identification in experiments because it creates statistical independence between treatment and potential outcomes any potential confounding factors

\[ Y_i(1),Y_i(0),\mathbf{X_i},\mathbf{U_i} \unicode{x2AEB} D_i \]

Randomization creates credible counterfactual comparisons

If treatment has been randomly assigned, then:

  • The only thing that differs between treatment and control is that one group got the treatment, and another did not.
  • We can estimate the Average Treatment Effect (ATE) using the difference of sample means

\[ \begin{aligned} E \left[ \frac{\sum_1^m Y_i}{m}-\frac{\sum_{m+1}^N Y_i}{N-m}\right]&=\overbrace{E \left[ \frac{\sum_1^m Y_i}{m}\right]}^{\substack{\text{Average outcome}\\ \text{among treated}\\ \text{units}}} -\overbrace{E \left[\frac{\sum_{m+1}^N Y_i}{N-m}\right]}^{\substack{\text{Average outcome}\\ \text{among control}\\ \text{units}}}\\ &= E [Y_i(1)|D_i=1] -E[Y_i(0)|D_i=0] \end{aligned} \]

Observational Designs

  • Observational designs are studies in which a causal variable of interest is determined by someone/thing other than the researcher (nature, governments, people, etc.)

  • Since treatment has not been randomly assigned, observational studies typically require stronger assumptions to make causal claims.

  • Generally speaking, these assumptions amount to a claim about conditional independence

\[ Y_i(1),Y_i(0),\mathbf{X_i},\mathbf{U_i} \unicode{x2AEB} D_i | K_i \]

  • Where after conditioning on \(K_i\), some knowledge about the world and how the data were generated, our treatment is as good as (as-if) randomly assigned (hence conditionally independent)
    • Economists often call this assumption of selection on observables

Causal Inference in Observational Studies

To understand how to make causal claims in observational studies we will:

  • Introduce the concept of Directed Acyclic Graphs to describe causal relationships

  • Discuss three approaches to covariate adjustment

    • Subclassification
    • Matching
    • Linear Regression

  • Three research designs for observational data

    • Differences-in-Differences
    • Regression Discontinuity Designs
    • Instrumental Variables

Directed Acyclic Graphs

Two Ways to Describe Causal Claims

In this course, we will use two forms of notation to describe our causal claims.

  • Potential Outcomes Notation (last lecture)

    • Illustrates the fundamental problem of causal inference

  • Directed Acyclic Graphs (DAGs)

    • Illustrates potential bias from confounders and colliders

Directed Acyclic Graphs

  • Directed Acyclic Graphs provide a way of encoding assumptions about casual relationships

    • Directed Arrows \(\to\) describe a direct causal effect

    • Arrow from \(D\to Y\) means \(Y_i(d) \neq Y_i(d^\prime)\) “The outcome ( \(Y\)) for person \(i\) when D happens ( \(Y_i(d)\) ) is different than the the outcome when \(D\) doesn’t happen ( \(Y_i(d^\prime)\) )

    • No arrow = no effect ( \(Y_i(d) = Y_i(d^\prime)\) )

    • Acyclic: No cycles. A variable can’t cause itself

Types of variables in a DAG

Blair, Coppock, and Humphreys (2023) (Chap. 6.2)

Causal Explanations Involve:

  • Y our outcome
  • D A possible cause of Y
  • M A mediator or mechanism through which D effects Y
  • Z An instrument that can help us isolate the effects of D on `Y
  • X2 a covariate that may moderate the effect of D on Y

Threats to causal claims/Sources of bias:

  • X1 an observed confounder that is a common cause of both D & Y
  • U an unobserved confounder a common cause of both D & Y
  • K a collider that is a common consequence of both D & Y

DAGs illustrate two sources of bias:

  • Confounder bias: Failing to control for a common cause of D and Y (aka Omitted Variable Bias)

  • Collider bias: Controlling for a common consequence (aka Selection Bias1)

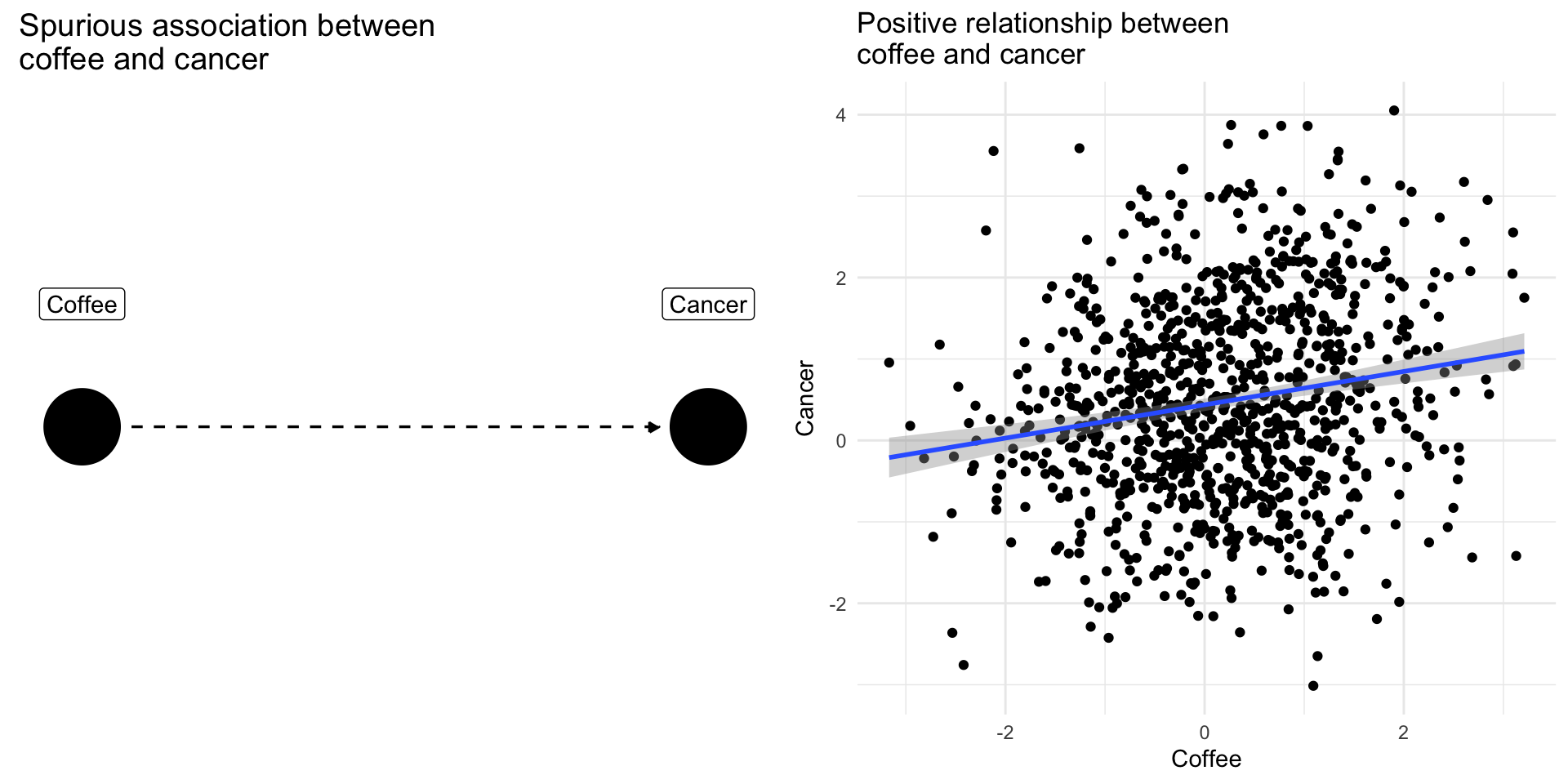
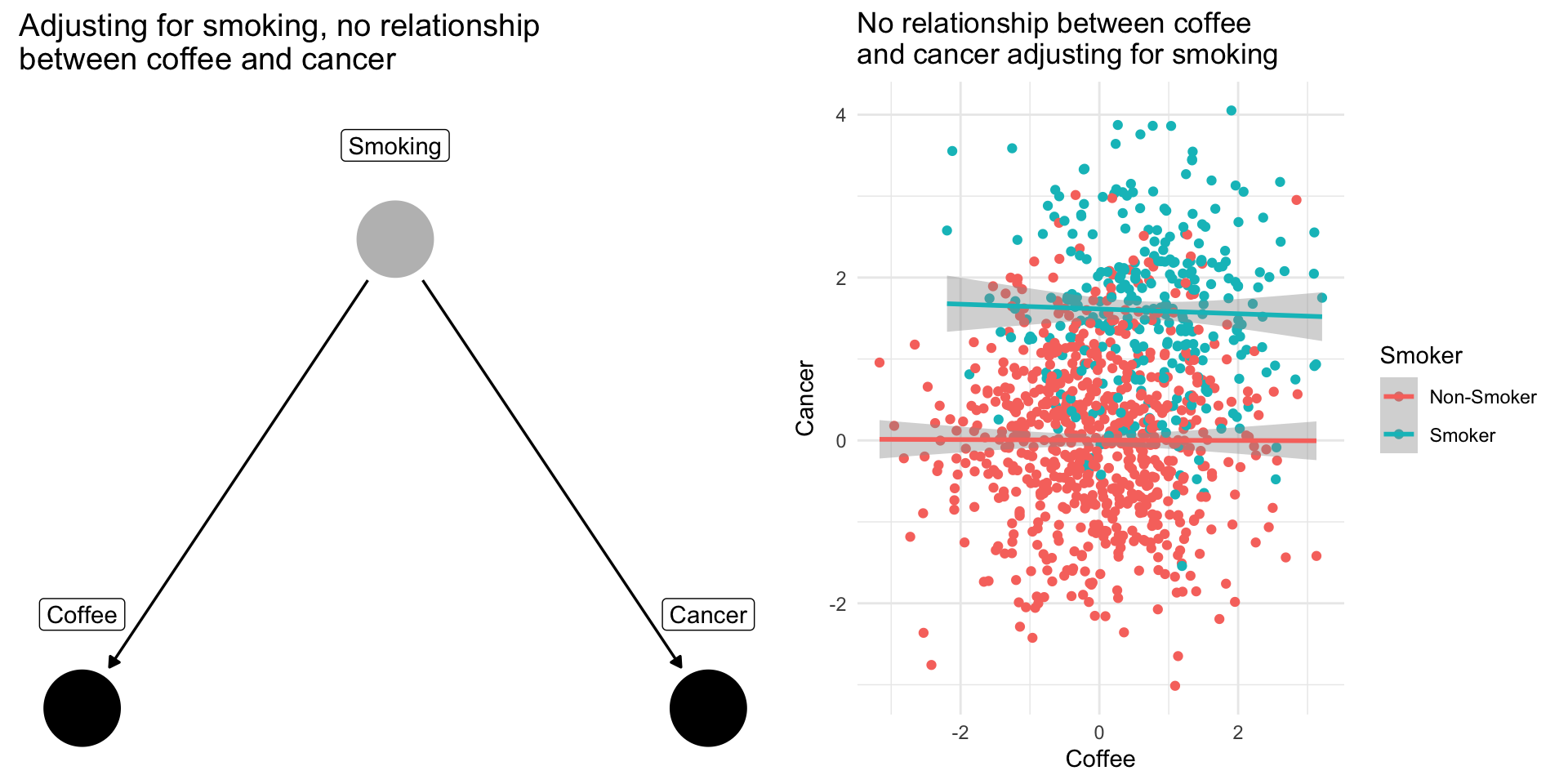
Confounding Bias: The Coffee Example

  • Drinking coffee doesn’t cause lung cancer we might find correlation between them because they share a common cause: smoking.

  • Smoking is a [confounding] variable, that if omitted will bias our results producing a spurious relationsip

  • [Adjusting] for [confounders] removes this source of bias

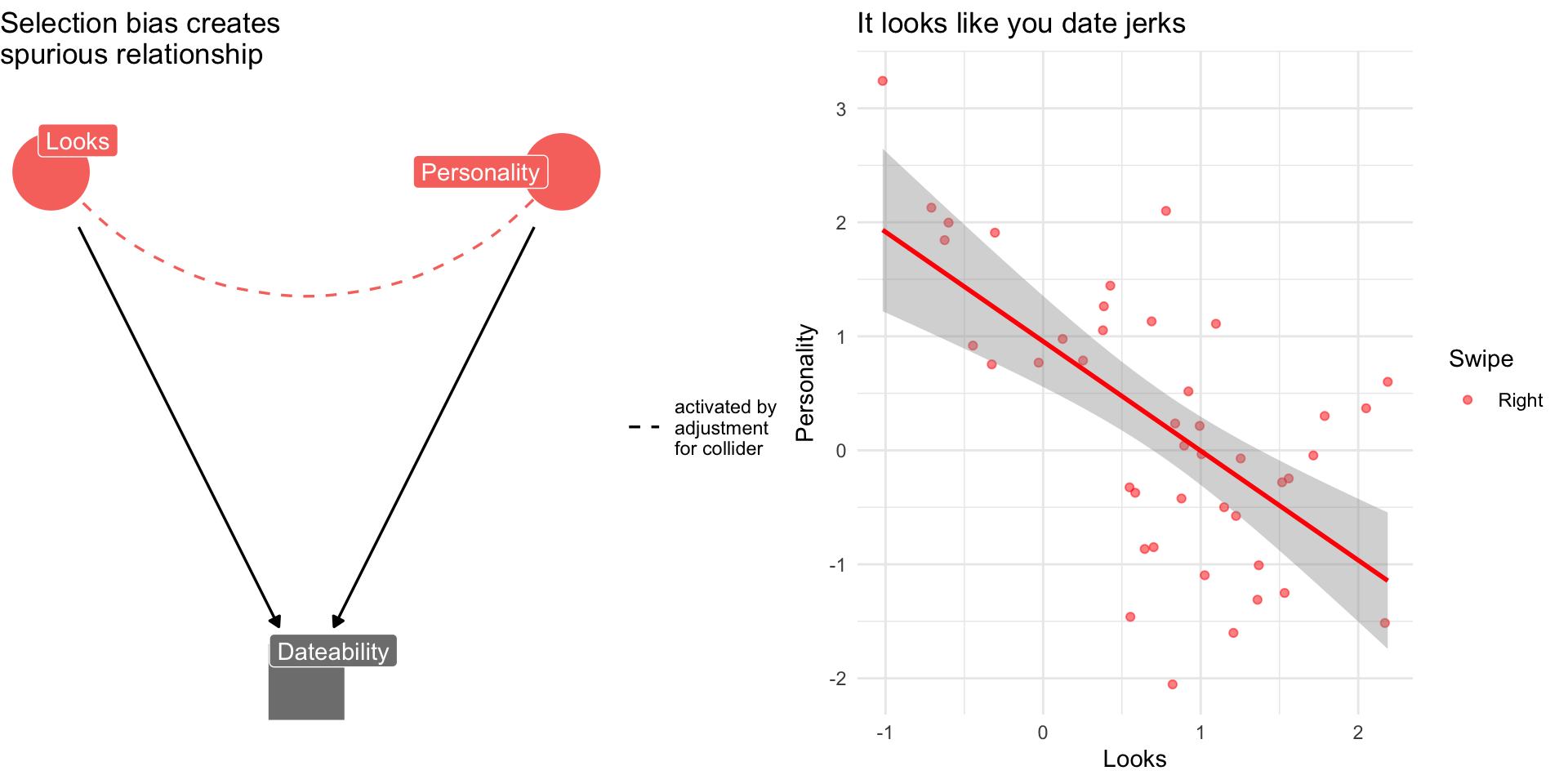
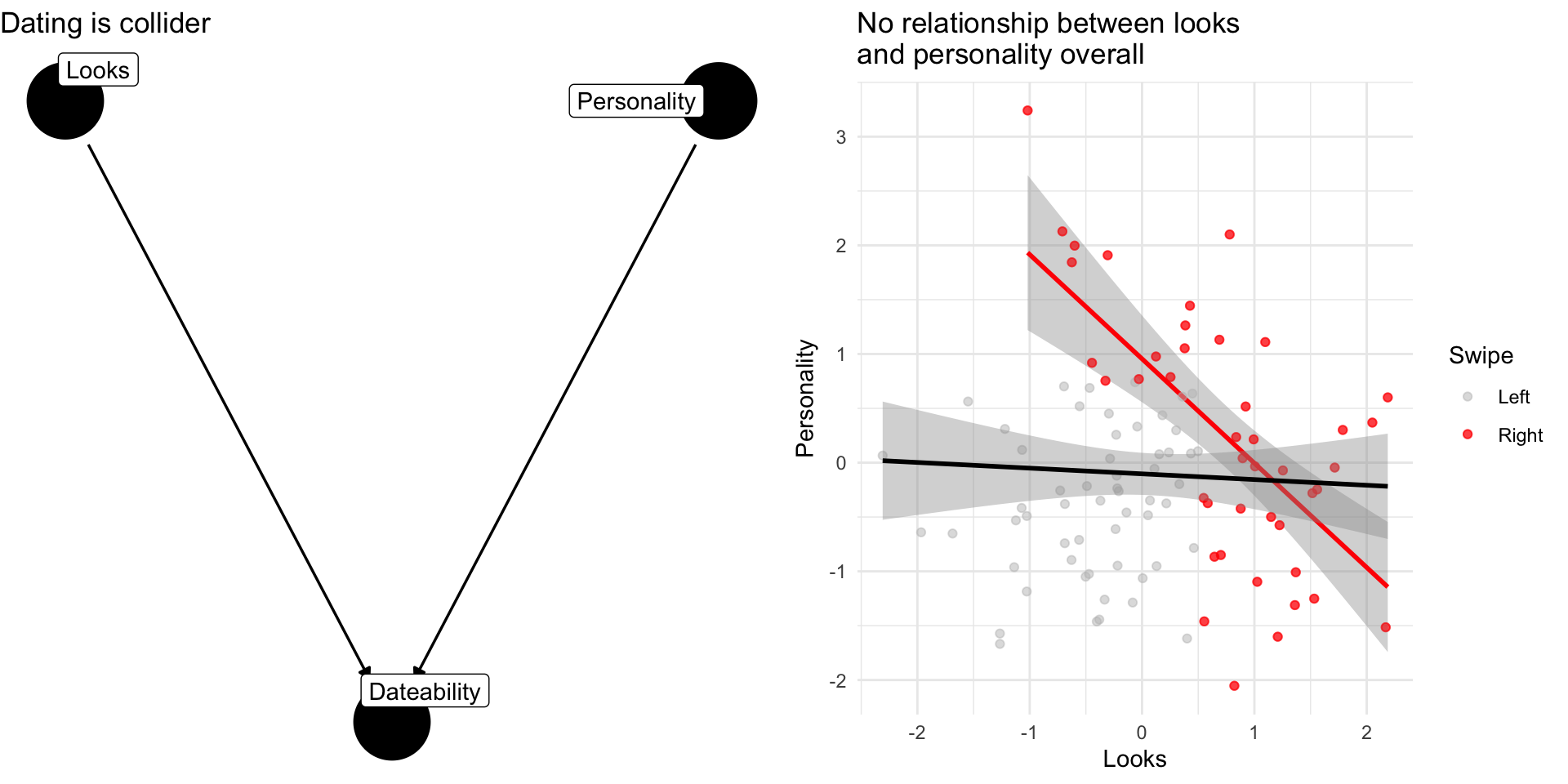
Collider Bias: The Dating Example

  • Why are attractive people such jerks?

  • Suppose dating is a function of looks and personality

  • Dating is a common consequences of looks and personality

  • Basing our claim off of who we date is an example of selection bias created by controlling for collider

When to control for a variable:

(Blair, Coppock, and Humphreys 2023) (Chap. 6.2)

Covariate Adjustment

Covariate Adjustment

Covariate adjustment refers a broad class of procedures that try to make a comparison more credible or meaningful by adjusting for some other potentially confounding factor.

Covariate Adjustment

When you hear people talk about

  • Controlling for age
  • Conditional on income
  • Holding age and income constant
  • Ceteris paribus (All else equal)

They are typically talking about some sort of covariate adjustment.

Three approaches to covariate adjustment

  • Subclassification
    • 👍: Easy to implement and interpret
    • 👎: Curse of dimensionality, Selection on observables
  • Matching
    • 👍: Balance on multiple covariates, Mirrors logic of experimental design
    • 👎: Selection on observables, Only provides balance on observed variables, Lot’s of technical details…
  • Regression
    • 👍: Easy to implement, control for many factors (good and bad)
    • 👎: Selection on observables, easy to fit “bad” models

Simple Linear Regression

Understanding Linear Regression

  • Conceptual
    • Simple linear regression estimates “a line of best fit” that summarizes relationships between two variables

\[ y_i = \beta_0 + \beta_1x_i + \epsilon_i \]

  • Practical
    • We estimate linear models in R using the lm() function
lm(y ~ x, data = df)

Understanding Linear Regression

  • Technical/Definitional
    • Linear regression chooses \(\beta_0\) and \(\beta_1\) to minimize the Sum of Squared Residuals (SSR):

\[\textrm{Find }\hat{\beta_0},\,\hat{\beta_1} \text{ arg min}_{\beta_0, \beta_1} \sum (y_i-(\beta_0+\beta_1x_i))^2\]

  • Theoretical
    • Linear regression provides a linear estimate of the conditional expectation function (CEF): \(E[Y|X]\)

Conceptual: Linear Regression

Conceptual: Linear Regression

  • Regression is a tool for describing relationships.

    • How does some outcome we’re interested in tend to change as some predictor of that outcome changes?

    • How does economic development vary with democracy?

    • How does economic development vary with democracy, adjusting for natural resources like oil and gas

Conceptual: Linear Regression

More formally:

\[ y_i = f(x_i) + \epsilon \]

  • Y is a function of X plus some error, \(\epsilon\)

  • Linear regression assumes that relationship between an outcome and a predictor can be by a linear function

\[ y_i = \beta_0 + \beta_1 x_i + \epsilon \]

Linear Regression and the Line of Best Fit

  • The goal of linear regression is to choose coefficients \(\beta_0\) and \(\beta_1\) to summarizes the relationship between \(y\) and \(x\)

\[ y_i = \beta_0 + \beta_1 x_i + \epsilon \]

  • To accomplish this we need some sort of criteria.

  • For linear regression, that criteria is minimizing the error between what our model predicts \(\hat{y_i} = \beta_0 + \beta_1 x_i\) and what we actually observed \((y_i)\)

  • More on this to come. But first…

Regression Notation

  • \(y_i\) an outcome variable or thing we’re trying to explain

    • AKA: The dependent variable, The response Variable, The left hand side of the model

  • \(x_i\) a predictor variables or things we think explain variation in our outcome

    • AKA: The independent variable, covariates, the right hand side of the model.

    • Cap or No Cap: I’ll use \(X\) (should be \(\mathbf{X}\)) to denote a set (matrix) of predictor variables. \(y\) vs \(Y\) can also have technical distinctions (Sample vs Population, observed value vs Random Variable, …)

  • \(\beta\) a set of unknown parameters that describe the relationship between our outcome \(y_i\) and our predictors \(x_i\)

  • \(\epsilon\) the error term representing variation in \(y_i\) not explained by our model.

Linear Regression

  • We call this a bivariate regression, because there are only two variables

\[ y_i = \beta_0 + \beta_1 x_i + \epsilon \]

  • We call this a linear regression, because \(y_i = \beta_0 + \beta_1 x_i\) is the equation for a line, where:

    • \(\beta_0\) corresponds to the \(y\) intercept, or the model’s prediction when \(x = 0\).

    • \(\beta_1\) corresponds to the slope, or how \(y\) is predicted to change as \(x\) changes.

Linear Regression

  • If you find this notation confusing, try plugging in substantive concepts for what \(y\) and \(x\) represent
  • Say we wanted to know how attitudes to transgender people varied with age in the baseline survey from Lab 03.

The generic linear model

\[y_i = \beta_0 + \beta_1 x_i + \epsilon\]

Reflects:

\[\text{Transgender Feeling Thermometer}_i = \beta_0 + \beta_1\text{Age}_i + \epsilon_i\]

Practical: Estimating a Linear Regression

Practical: Estimating a Linear Regression

  • We estimate linear regressions in R using the lm() function.
  • lm() requires two arguments:
    • a formula argument of the general form y ~ x read as “Y modeled by X” or below “Transgender Feeling Thermometer (y) modeled by (~) Age (x)
    • a data argument telling R where to find the variables in the formula
load(url("https://pols1600.paultesta.org/files/data/03_lab.rda"))
m1 <- lm(therm_trans_t0 ~ vf_age, data = df)
m1

Call:
lm(formula = therm_trans_t0 ~ vf_age, data = df)

Coefficients:
(Intercept)       vf_age  
    62.8196      -0.2031

The lm() function

The coefficients from lm() are saved in object called m1

m1

Call:
lm(formula = therm_trans_t0 ~ vf_age, data = df)

Coefficients:
(Intercept)       vf_age  
    62.8196      -0.2031

m1 actually contains a lot of information

names(m1)
 [1] "coefficients"  "residuals"     "effects"       "rank"         
 [5] "fitted.values" "assign"        "qr"            "df.residual"  
 [9] "na.action"     "xlevels"       "call"          "terms"        
[13] "model"        
m1$coefficients
(Intercept)      vf_age 
 62.8195994  -0.2030711

Practical: Interpreting a Linear Regression

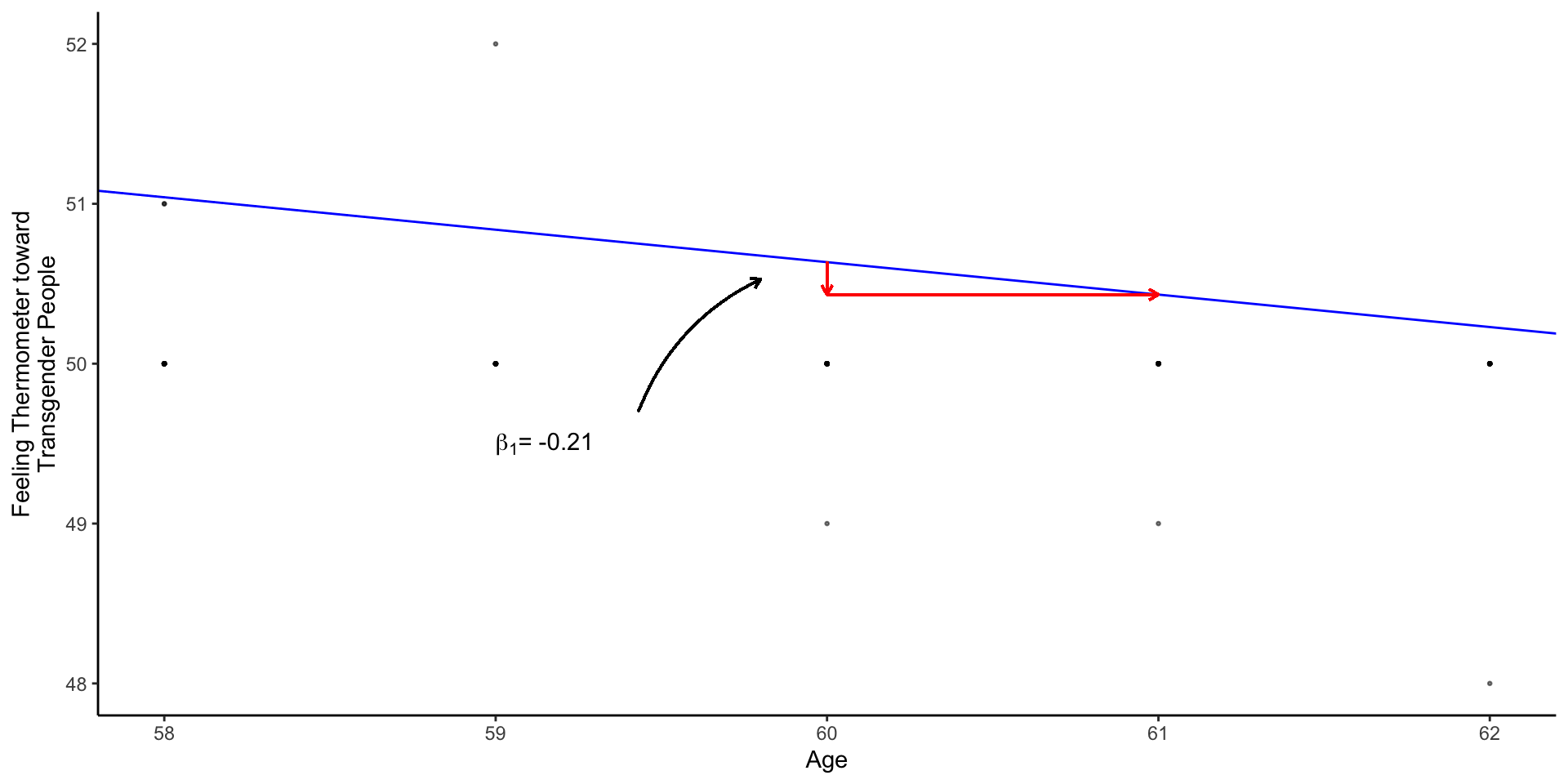
We can extract the intercept and slope from this simple bivariate model, using the coef() function

# All the coefficients
coef(m1)
(Intercept)      vf_age 
 62.8195994  -0.2030711 
# Just the intercept
coef(m1)[1]
(Intercept) 
    62.8196 
# Just the slope
coef(m1)[2]
    vf_age 
-0.2030711

Practical: Interpreting a Linear Regression

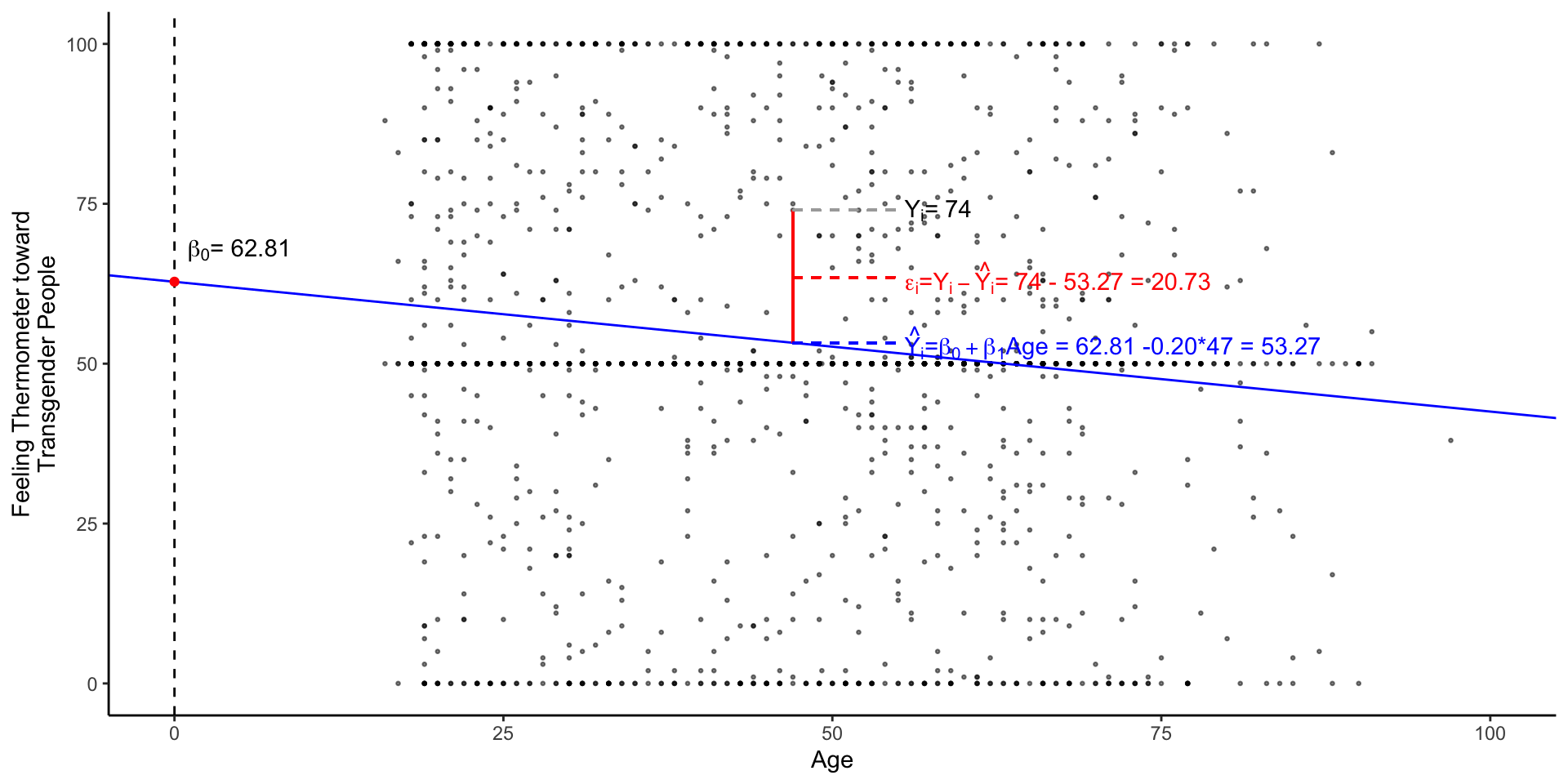
The two coefficients from m1 define a line of best fit, summarizing how feelings toward transgender individuals change with age

\[y_i = \beta_0 + \beta_1 x_i + \epsilon\]

\[\text{Transgender Feeling Thermometer}_i = \beta_0 + \beta_1\text{Age}_i + \epsilon_i\]

\[\text{Transgender Feeling Thermometer}_i = 62.82 + -0.2 \text{Age}_i + \epsilon_i\]

Practical: Predicted values from a Linear Regression

  • Often it’s useful for interpretation to obtain predicted values from a regression.

  • To obtain predicted vales \((\hat{y})\), we simply plug in a value for \(x\) (In this case, \(Age\)) and evaluate our equation.

  • For example, might we expect attitudes to differ among an 18-year-old college student and their 68-year-old grandparent?

\[\hat{FT}_{x=18} = 62.82 + -0.2 \times 18 = 59.16\] \[\hat{FT}_{x=65} = 62.82 + -0.2 \times 68 = 49.01\]

Practical: Predicted values from a Linear Regression

We could do this by hand

coef(m1)[1] + coef(m1)[2] * 18
(Intercept) 
   59.16432 
coef(m1)[1] + coef(m1)[2] * 68
(Intercept) 
   49.01076

Practical: Predicted values from a Linear Regression

More often we will:

  • Make a prediction data frame (called pred_df below) with the values of interests
  • Use the predict() function with our linear model (m1) and pred_df
  • Save the predicted values to our new column in our prediction data frame

Practical: Predicted values from a Linear Regression

# Make prediction data frame
pred_df <- data.frame(
  vf_age = c(18, 68)
)
# Predict FT for 18 and 68 year-olds
predict(m1, newdata = pred_df)
       1        2 
59.16432 49.01076 
# Save predictions to data frame
pred_df$ft_trans_hat <- predict(m1, newdata = pred_df)
pred_df
  vf_age ft_trans_hat
1     18     59.16432
2     68     49.01076

Practical: Visualizing Linear Regression

We can visualize simple regression by:

  • plotting a scatter plot of the outcome (y-axis) and predictors (x-axis)

  • overlaying the line defined by lm()

fig_lm <- df %>%
  ggplot(aes(vf_age,therm_trans_t0))+
  geom_point(size=.5, alpha=.5)+
  geom_abline(intercept = coef(m1)[1],
              slope = coef(m1)[2],
              col = "blue"
              )+
  geom_vline(xintercept = 0,linetype = 2)+
  xlim(0,100)+
  annotate("point",
           x = 0, y = coef(m1)[1],
           col= "red",
           )+
  annotate("text",
           label = expression(paste(beta[0],"= 62.81" )),
           x = 1, y = coef(m1)[1]+5,
           hjust = "left",
           )+
  labs(
    x = "Age",
    y = "Feeling Thermometer toward\nTransgender People"
  )+
  theme_classic() -> fig_lm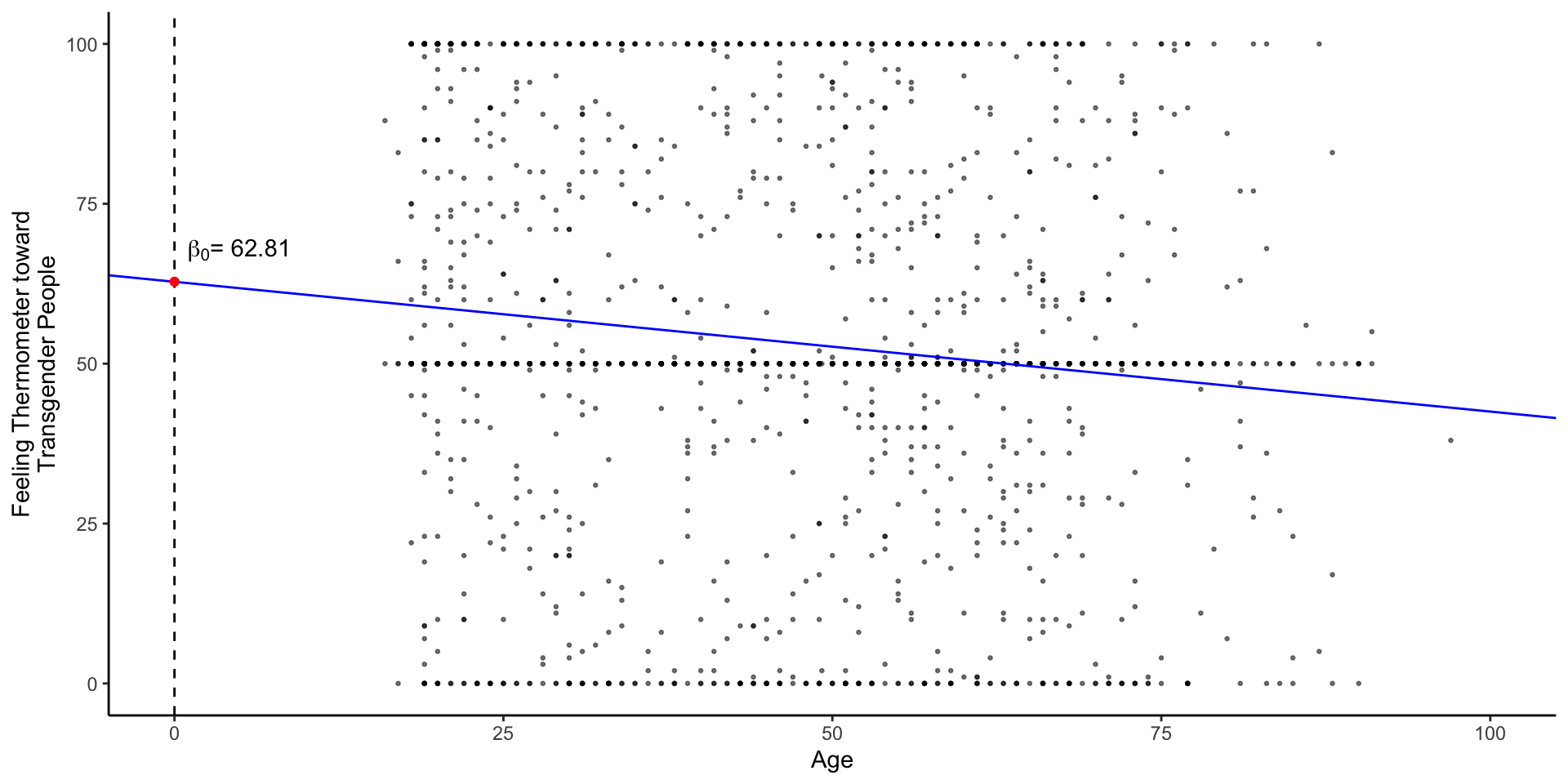

Technichal: Mechanics of Linear Regression

How did lm() choose \(\beta_0\) and \(\beta_1\)

  • P: By minimizing the sum of squared errors, in procedure called Ordinary Least Squares (OLS) regression

  • Q: Ok, that’s not really that helpful…

    • What’s an error?
    • Why would we square and sum them
    • How do we minimize them.

P: Good questions!

What’s an error?

An error, \(\epsilon_i\) is simply the difference between the observed value of \(y_i\) and what our model would predict, \(\hat{y_i}\) given some value of \(x_i\). So for a model:

\[y_i=\beta_0+\beta_1 x_{i} + \epsilon_i\]

We simply subtract our model’s prediction \(\beta_0+\beta_1 x_{i}\) from the the observed value, \(y_i\)

\[\hat{\epsilon_i}=y_i-\hat{y_i}=(Y_i-(\beta_0+\beta_1 x_{i}))\]

To get \(\epsilon_i\)

Why are we squaring and summing \(\epsilon\)

There are more mathy reasons for this, but at intuitive level, the Sum of Squared Residuals (SSR)

  • Squaring \(\epsilon\) treats positive and negative residuals equally.

  • Summing produces single value summarizing our models overall performance.

There are other criteria we could use (e.g. minimizing the sum of absolute errors), but SSR has some nice properties

How do we minimize \(\sum \epsilon^2\)

OLS chooses \(\beta_0\) and \(\beta_1\) to minimize \(\sum \epsilon^2\), the Sum of Squared Residuals (SSR)

\[\textrm{Find }\hat{\beta_0},\,\hat{\beta_1} \text{ arg min}_{\beta_0, \beta_1} \sum (y_i-(\beta_0+\beta_1x_i))^2\]

How did lm() choose \(\beta_0\) and \(\beta_1\)

In an intro stats course, we would walk through the process of finding

\[\textrm{Find }\hat{\beta_0},\,\hat{\beta_1} \text{ arg min}_{\beta_0, \beta_1} \sum (y_i-(\beta_0+\beta_1x_i))^2\] Which involves a little bit of calculus. The big payoff is that

\[\beta_0 = \bar{y} - \beta_1 \bar{x}\] And

\[ \beta_1 = \frac{Cov(x,y)}{Var(x)}\] Which is never quite the epiphany, I think we think it is…

The following slides walk you through the mechanics of this exercise. We’re gonna skip through them in class, but they’re there for your reference

How do we minimize \(\sum \epsilon^2\)

To understand what’s going on under the hood, you need a broad understanding of some basic calculus.

The next few slides provide a brief review of derivatives and differential calculus.

Derivatives

The derivative of \(f\) at \(x\) is its rate of change at \(x\)

  • For a line: the slope
  • For a curve: the slope of a line tangent to the curve

You’ll see two notations for derivatives:

  1. Leibniz notation:

\[ \frac{df}{dx}(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{(x+h)-x} \]

  1. Lagrange: \(f^{\prime}(x)\)

Some useful Facts about Derivatives

Derivative of a constant

\[ f^{\prime}(c)=0 \]

Derivative of a line f(x)=2x

\[ f^{\prime}(2x)=2 \]

Derivative of \(f(x)=x^2\)

\[ f^{\prime}(x^2)=2x \]

Chain rule: y= f(g(x)). The derivative of y with respect to x is

\[ \frac{d}{dx}(f(g(x)))=f^{\prime}(g(x))g^{\prime}(x) \]

The derivative of the “outside” times the derivative of the “inside,” remembering that the derivative of the outside function is evaluated at the value of the inside function.

Finding a Local Minimums

Local minimum:

\[ f^{\prime}(x)=0 \text{ and } f^{\prime\prime}(x)>0 \]

Source

Partial Derivatives

Let \(f\) be a function of the variables \((x, \dots, X_n)\). The partial derivative of \(f\) with respect to \(X_i\) is

\[\begin{align*} \frac{\partial f(x, \dots, X_n)}{\partial X_i}=\lim_{h\to0}\frac{f(x, \dots X_i+h \dots, X_n)-f(x, \dots X_i \dots, X_n)}{h} \end{align*}\]

Source

Minimizing the sum of squared errors

Our model

\[y_i =\beta_0+\beta_1x_{i}+\epsilon_i\]

Finds coefficients \(\beta_0\) and \(\beta_1\) to to minimize the sum of squared residuals, \(\hat{\epsilon}_i\):

\[\begin{aligned} \sum \hat{\epsilon_i}^2 &= \sum (y_i-\beta_0-\beta_1 x_{i})^2 \end{aligned}\]

Minimizing the sum of squared errors

We solve for \(\beta_0\) and \(\beta_1\), by taking the partial derivatives with respect to \(\beta_0\) and \(\beta_1\), and setting them equal to zero

\[\begin{aligned} \frac{\partial \sum \hat{\epsilon_i}^2}{\partial \beta_0} &= -2\sum (y_i-\beta_0-\beta_1 x_{i})=0 & f'(-x^2) = -2x\\ \frac{\partial \sum \hat{\epsilon_i}^2}{\partial\beta_1} &= -2\sum (y_i-\beta_0-\beta_1 x_{i})x_{i}=0 & \text{chain rule} \end{aligned}\]

Solving for \(\beta_0\)

First, we’ll solve for \(\beta_0\), by multiplying both sides by -1/2 and distributing the \(\sum\):

\[\begin{aligned} 0 &= -2\sum (y_i-\beta_0-\beta_1 x_{i})\\ \sum \beta_0 &= \sum y_i - \sum \beta_1 x_{i}\\ N \beta_0 &= \sum y_i -\sum \beta_1 x_{i}\\ \beta_0 &= \frac{\sum y_i}{N} - \frac{\beta_1 \sum x_{i}}{N}\\ \beta_0 &= \bar{y} - \beta_1 \bar{x} \end{aligned}\]

Solving for \(\beta_1\)

Now, we can solve for \(\beta_1\) plugging in \(\beta_0\).

\[\begin{aligned} 0 &= -2\sum [(y_i-\beta_0-\beta_1 x_{i})x_{i}]\\ 0 &= \sum [y_ix_i-(\bar{y} - \beta_1 \bar{x})x_{i}-\beta_1 x_{i}^2]\\ 0 &= \sum [y_ix_i-\bar{y}x_{i} + \beta_1 \bar{x}x_{i}-\beta_1 x_{i}^2] \end{aligned}\]

Solving for \(\beta_1\)

Now we’ll rearrange some terms and pull out an \(x_{i}\) to get

\[\begin{aligned} 0 &= \sum [(y_i -\bar{y} + \beta_1 \bar{x}-\beta_1 x_{i})x_{i}] \end{aligned}\]

Dividing both sides by \(x_{i}\) and distributing the summation, we can isolate \(\beta_1\)

\[\begin{aligned} \beta_1 \sum (x_{i}-\bar{x}) &= \sum (y_i -\bar{y}) \end{aligned}\]

Dividing by \(\sum (x_{i}-\bar{x})\) to get

\[\begin{aligned} \beta_1 &= \frac{\sum (y_i -\bar{y})}{\sum (x_{i}-\bar{x})} \end{aligned}\]

Solving for \(\beta_1\)

Finally, by multiplying by \(\frac{(x_{i}-\bar{x})}{(x_{i}-\bar{x})}\) we get

\[\begin{aligned} \beta_1 &= \frac{\sum (y_i -\bar{y})(x_{i}-\bar{x})}{\sum (\bar{x}-x_{i})^2} \end{aligned}\]

Which has a nice interpretation:

\[\begin{aligned} \beta_1 &= \frac{Cov(x,y)}{Var(x)} \end{aligned}\]

So the coefficient in a simple linear regression of \(Y\) on \(X\) is simply the ratio of the covariance between \(X\) and \(Y\) over the variance of \(X\). Neat!

Theoretical: OLS provides a linear estimate of CEF: E[Y|X]

Linear Regression is a many splendored thing

Timothy Lin provides a great overview of the various interpretations/motivations for linear regression.

Linear Regression is a many splendored thing

Timothy Lin provides a great overview of various interpretations/motivations for linear regression.

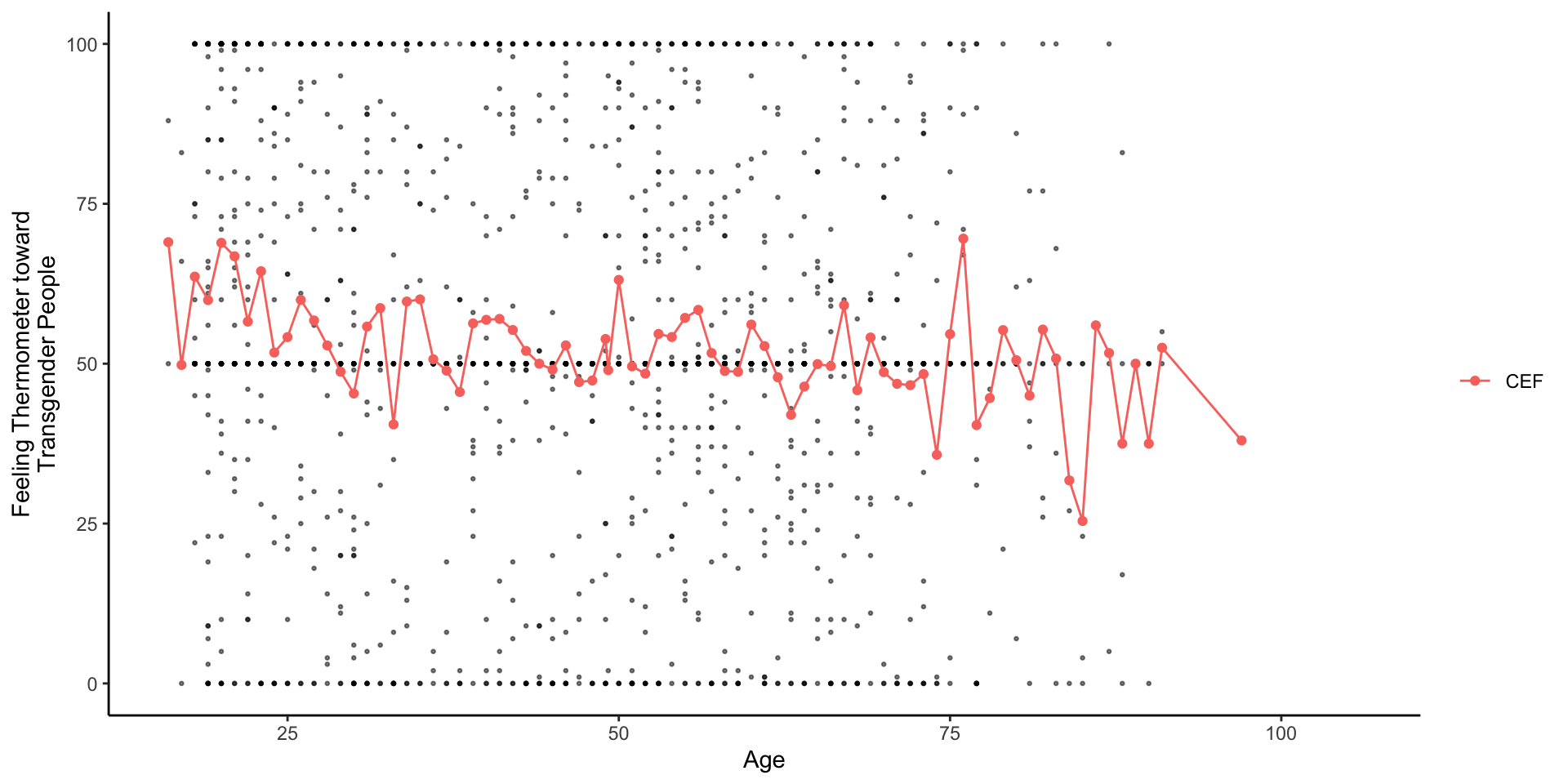
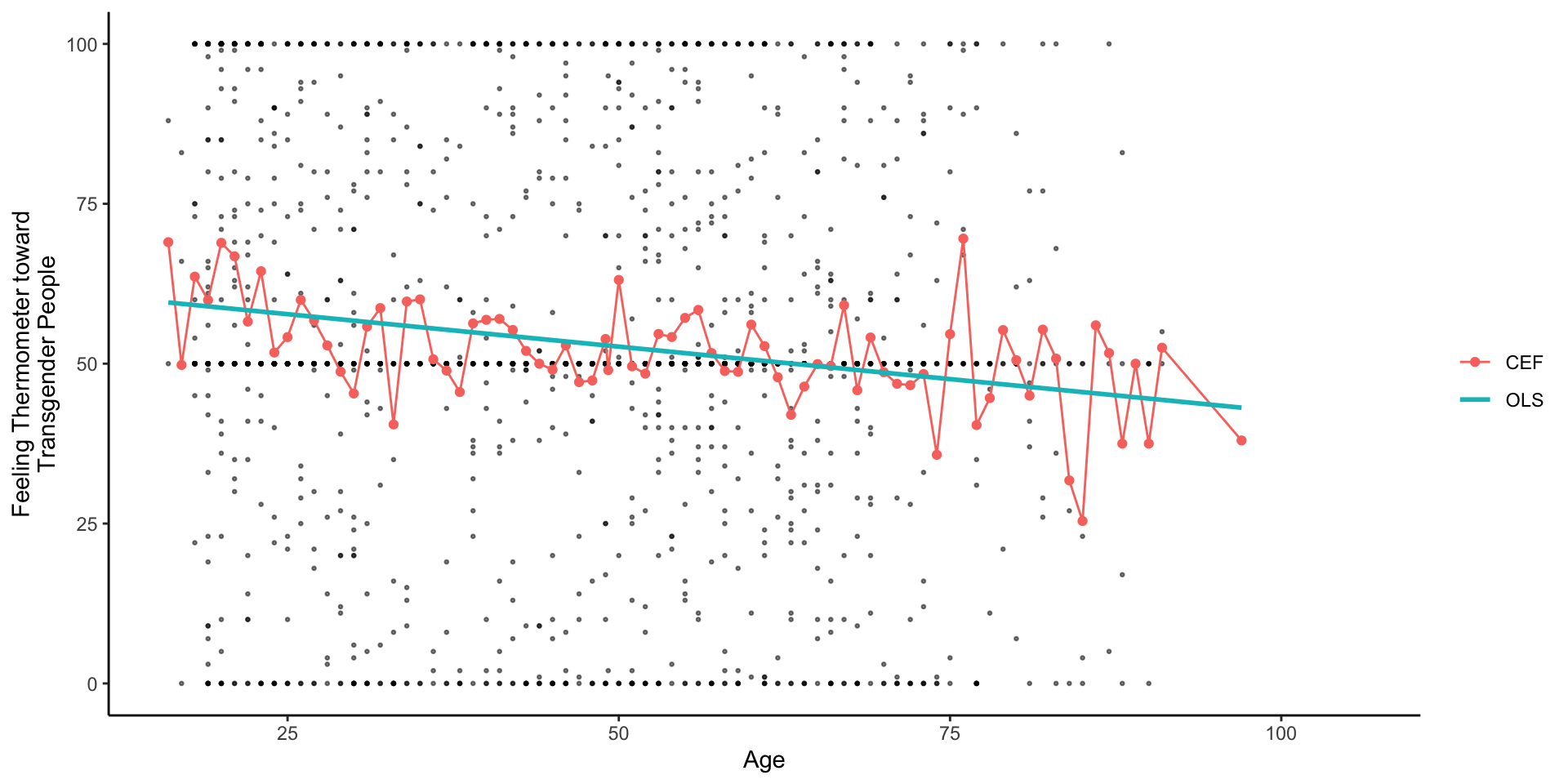
The Conditional Expectation Function

Of all the functions we could choose to describe the relationship between \(Y\) and \(X\),

\[ Y_i = f(X_i) + \epsilon_i \]

the conditional expectation of \(Y\) given \(X\) \((E[Y|X])\), has some appealing properties

\[ Y_i = E[Y_i|X_i] + \epsilon \]

The error, by definition, is uncorrelated with X and \(E[\epsilon|X]=0\)

\[ E[\epsilon|X] = E[Y - E[Y|X]|X]= E[Y|X] - E[Y|X] = 0 \]

Of all the possible functions \(g(X)\), we can show that \(E[Y_i|X_i]\) is the best predictor in terms of minimizing mean squared error

\[ E[ (Y - g(Y))^2] \geq E[(Y - E[Y|X])^2] \]

Linear Approximations to the Conditional Expectation Function

What you need to know about Regression

  • Conceptual
    • Simple linear regression estimates a line of best fit that summarizes relationships between two variables

\[ y_i = \beta_0 + \beta_1x_i + \epsilon_i \]

  • Practical
    • We estimate linear models in R using the lm() function
lm(y ~ x, data = df)

What you need to know about Regression

  • Technical/Definitional
    • Linear regression chooses \(\beta_0\) and \(\beta_1\) to minimize the Sum of Squared Residuals (SSR):

\[\textrm{Find }\hat{\beta_0},\,\hat{\beta_1} \text{ arg min}_{\beta_0, \beta_1} \sum (y_i-(\beta_0+\beta_1x_i))^2\]

  • Theoretical
    • Linear regression provides a linear estimate of the conditional expectation function (CEF): \(E[Y|X]\)

Difference-in-Differences

Motivating Example: What causes Cholera?

  • In the 1800s, cholera was thought to be transmitted through the air.

  • John Snow (the physician, not the snack), to explore the origins eventunally concluding that cholera was transmitted through living organisms in water.

  • Leveraged a natural experiment in which one water company in London moved its pipes further upstream (reducing contamination for Lambeth), while other companies kept their pumps serving Southwark and Vauxhall in the same location.

Notation

Let’s adopt a little notation to help us think about the logic of Snow’s design:

  • \(D\): treatment indicator, 1 for treated neighborhoods (Lambeth), 0 for control neighborhoods (Southwark and Vauxhall)

  • \(T\): period indicator, 1 if post treatment (1854), 0 if pre-treatment (1849).

  • \(Y_{di}(t)\) the potential outcome of unit \(i\)

    • \(Y_{1i}(t)\) the potential outcome of unit \(i\) when treated between the two periods

    • \(Y_{0i}(t)\) the potential outcome of unit \(i\) when control between the two periods

Causal Effects

The individual causal effect for unit i at time t is:

\[\tau_{it} = Y_{1i}(t) − Y_{0i}(t)\]

What we observe is

\[Y_i(t) = Y_{0i}(t)\cdot(1 − D_i(t)) + Y_{1i}(t)\cdot D_i(t)\]

\(D\) only equals 1, when \(T\) equals 1, so we never observe \(Y_0i(1)\) for the treated units.

In words, we don’t know what Lambeth’s outcome would have been in the second period, had they not been treated.

Average Treatment on Treated

Our goal is to estimate the average effect of treatment on treated (ATT):

\[\tau_{ATT} = E[Y_{1i}(1) - Y_{0i}(1)|D=1]\]

That is, what would have happened in Lambeth, had their water company not moved their pipes

Average Treatment on Treated

Our goal is to estimate the average effect of treatment on treated (ATT):

We we can observe is:

Pre-Period (T=0) Post-Period (T=1)
Treated \(D_{i}=1\) \(E[Y_{0i}(0)\vert D_i = 1]\) \(E[Y_{1i}(1)\vert D_i = 1]\)
Control \(D_i=0\) \(E[Y_{0i}(0)\vert D_i = 0]\) \(E[Y_{0i}(1)\vert D_i = 0]\)

Data

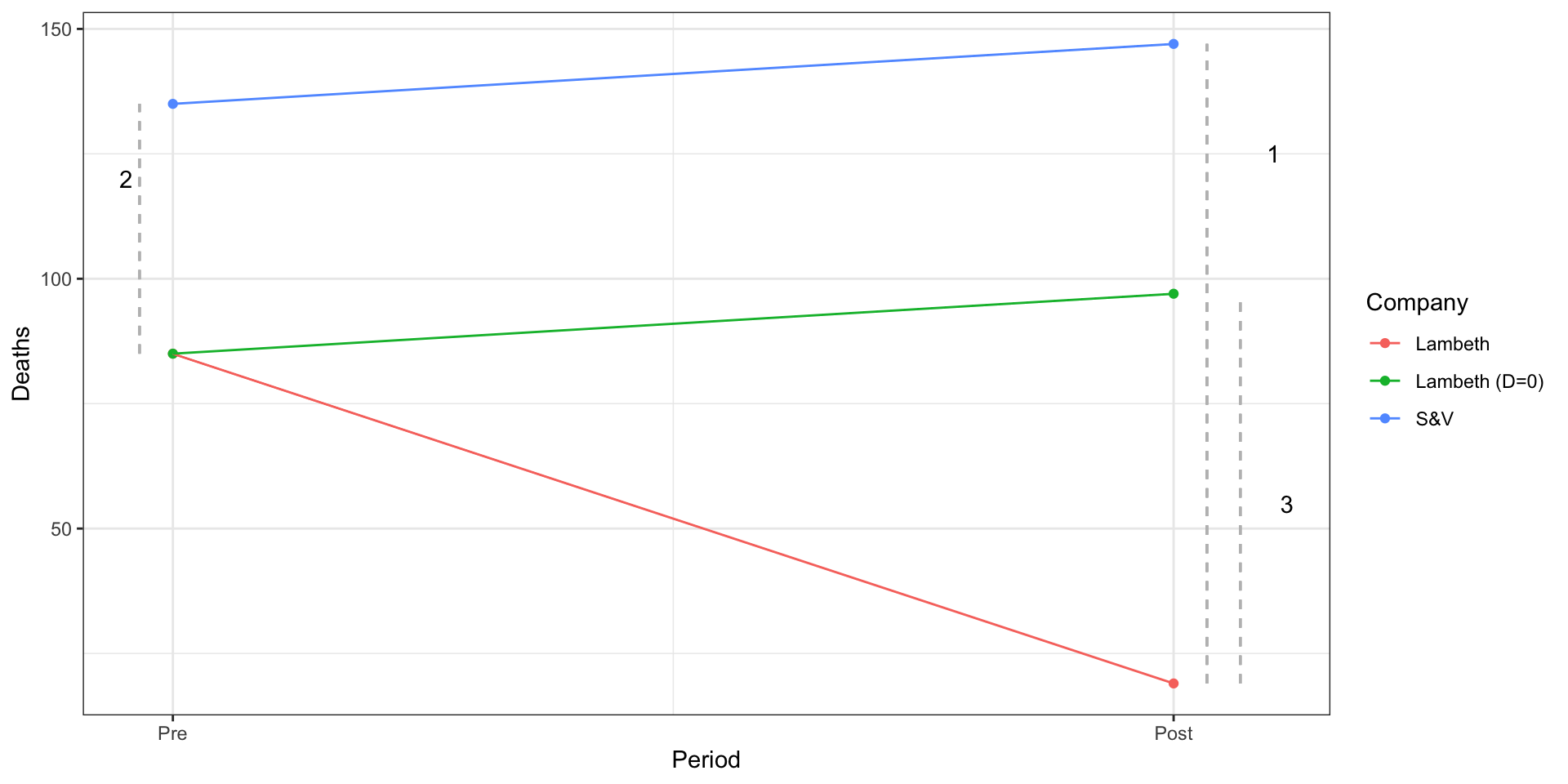
Because potential outcomes notation is abstract, let’s consider a modified description of the Snow’s cholera death data from Scott Cunningham:

Company 1849 (T=0) 1854 (T=1)
Lambeth (D=1) 85 19
Southwark and Vauxhall (D=0) 135 147

How can we estimate the effect of moving pumps upstream?

Recall, our goal is to estimate the effect of the the treatment on the treated:

\[\tau_{ATT} = E[Y_{1i}(1) - Y_{0i}(1)|D=1]\]

Let’s conisder some strategies Snow could take to estimate this quantity:

Before vs after comparisons:

  • Snow could have compared Labmeth in 1854 \((E[Y_i(1)|D_i = 1] = 19)\) to Lambeth in 1849 \((E[Y_i(0)|D_i = 1]=85)\), and claimed that moving the pumps upstream led to 66 fewer cholera deaths.

  • Assumes Lambeth’s pre-treatment outcomes in 1849 are a good proxy for what its outcomes would have been in 1954 if the pumps hadn’t moved \((E[Y_{0i}(1)|D_i = 1])\).

  • A skeptic might argue that Lambeth in 1849 \(\neq\) Lambeth in 1854

Company 1849 (T=0) 1854 (T=1)
Lambeth (D=1) 85 19
Southwark and Vauxhall (D=0) 135 147

Treatment-Control comparisons in the Post Period.

  • Snow could have compared outcomes between Lambeth and S&V in 1954 (\(E[Yi(1)|Di = 1] − E[Yi(1)|Di = 0]\)), concluding that the change in pump locations led to 128 fewer deaths.

  • Here the assumption is that the outcomes in S&V and in 1854 provide a good proxy for what would have happened in Lambeth in 1954 had the pumps not been moved \((E[Y_{0i}(1)|D_i = 1])\)

  • Again, our skeptic could argue Lambeth \(\neq\) S&V

Company 1849 (T=0) 1854 (T=1)
Lambeth (D=1) 85 19
Southwark and Vauxhall (D=0) 135 147

Difference in Differences

To address these concerns, Snow employed what we now call a difference-in-differences design,

There are two, equivalent ways to view this design.

\[\underbrace{\{E[Y_{i}(1)|D_{i} = 1] − E[Y_{i}(1)|D_{i} = 0]\}}_{\text{1. Treat-Control |Post }}− \overbrace{\{E[Y_{i}(0)|D_{i} = 1] − E[Y_{i}(0)|D_{i}=0 ]}^{\text{Treated-Control|Pre}}\]

  • Difference 1: Average change between Treated and Control in Post Period

  • Difference 2: Average change between Treated and Control in Pre Period

Difference in Differences

\[\underbrace{\{E[Y_{i}(1)|D_{i} = 1] − E[Y_{i}(1)|D_{i} = 0]\}}_{\text{1. Treat-Control |Post }}− \overbrace{\{E[Y_{i}(0)|D_{i} = 1] − E[Y_{i}(0)|D_{i}=0 ]}^{\text{Treated-Control|Pre}}\] Is equivalent to:

\[\underbrace{\{E[Y_{i}(1)|D_{i} = 1] − E[Y_{i}(0)|D_{i} = 1]\}}_{\text{Post - Pre |Treated }}− \overbrace{\{E[Y_{i}(1)|D_{i} = 0] − E[Y_{i}(0)|D_{i}=0 ]}^{\text{Post-Pre|Control}}\]

  • Difference 1: Average change between Treated over time
  • Difference 2: Average change between Control over time

Difference in Differences

You’ll see the DiD design represented both ways, but they produce the same result:

\[ \tau_{ATT} = (19-147) - (85-135) = -78 \]

\[ \tau_{ATT} = (19-85) - (147-135) = -78 \]

Identifying Assumption of a Difference in Differences Design

The key assumption in this design is what’s known as the parallel trends assumption: \(E[Y_{0i}(1) − Y_{0i}(0)|D_i = 1] = E[Y_{0i}(1) − Y_{0i}(0)|D_i = 0]\)

  • In words: If Lambeth hadn’t moved its pumps, it would have followed a similar path as S&V

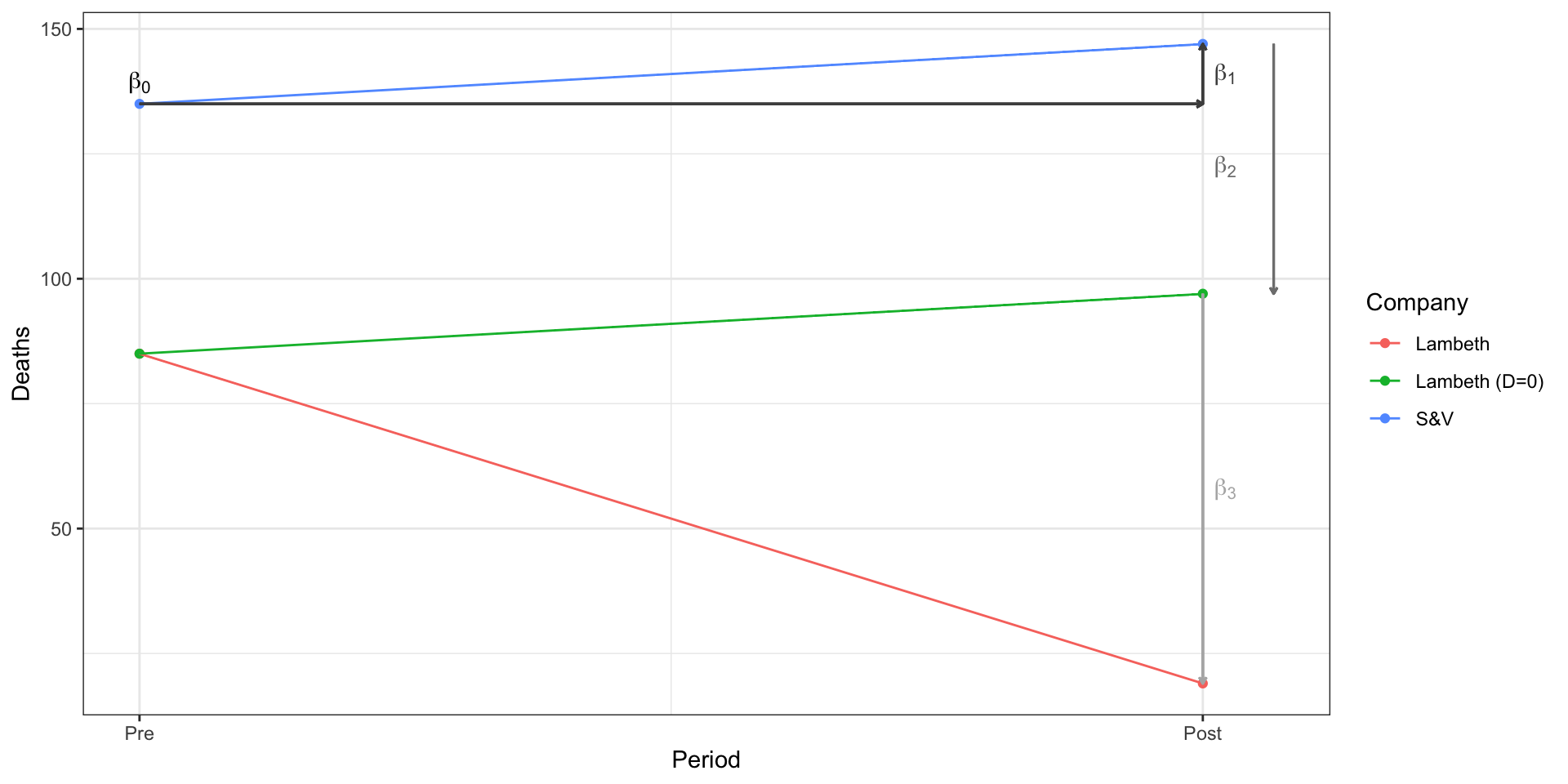
Summary

  • A Difference in Differences (DiD, or diff-in-diff) design combines a pre-post comparison, with a treated and control comparison

    • Taking the pre-post difference removes any fixed differences between the units

    • Then taking the difference between treated and control differences removes any common differences over time

  • The key identifying assumption of a DiD design is the “assumption of parallel trends”

    • Absent treatment, treated and control groups would see the same changes over time.
    • Hard to prove, possible to test

Extensions and limitations

  • Diff-in-Diff easy to estimate with linear regression
  • Generalizes to multiple periods and treatment interventions
    • More pre-treatment periods allow you assess “parallel trends” assumption
  • Alternative methods
    • Synthetic control
    • Event Study Designs
  • What if you have multiple treatments or treatments that come and go?
    • Panel Matching
    • Generalized Synthetic control

Applications

References

POLS 1600

Blair, Graeme, Alexander Coppock, and Macartan Humphreys. 2023. Research Design in the Social Sciences: Declaration, Diagnosis, and Redesign. Princeton University Press.