Lab 06 - Examining Alternative Explanations for Red Covid

How to have an argument with regression

Author

Your Group Members Names Here

Published

March 5, 2024

Overview

Today we will explore the critiques and alternative explanations for the phenomena of “Red Covid” discussed by the NYT’s David Leonhardt in articles last fall here and more recently here.

Recall the core thesis of Red Covid is something like the following:

Since Covid-19 vaccines became widely available to the general public in the spring of 2021, Republicans have been less likely to get the vaccine. Lower rates of vaccination among Republicans have in turn led to higher rates of death from Covid-19 in Red States compared to Blue States.

A skeptic of this claim might argue that relationship between electoral and epidemelogical outcomes is spurious, saying somthing like:

There are lots of ways that Red States differ from Blue States — demographics, economics, geography, culture, and so on – and it is these differences that explain the phenomena of Red Covid. If we were to control for these omitted variables the relationship between a state’s partisan leanings and Covid-19 would go away.

In this lab, we will see how we can explore these claims using multiple regression to control for competing explanations.

To accomplish this we will:

  1. Get set up to work (10 minutes)

Then we will estimate and interpret a series of regression models:

  1. A baseline Red Covid model using simple bivariate regression using the Republican vote share of states to predict the 14-day average of per capita Covid-19 deaths on September 23, 2021 (10 Minutes)

  2. A multiple regression model controlling for Republican vote share the median age (15 minutes)

  3. A model controlling for Republican vote share, the median age and median income (15 minutes)

  4. A model controlling for Republican vote share, the median age median income and vaccination rates (15 minutes)

  5. A model using Republican vote share, the median age median income to predict vaccination rates (15 minutes)

Finally, we’ll take the weekly survey which will serve as a mid semester check in.

One of these 6 tasks (excluding the weekly survey) will be randomly selected as the graded question for the lab.

set.seed(3052024)
graded_question <- sample(1:6,size = 1)
paste("Question",graded_question,"is the graded question for this week")
[1] "Question 4 is the graded question for this week"

You will work in your assigned groups. Only one member of each group needs to submit the html file of lab.

This lab must contain the names of the group members in attendance.

If you are attending remotely, you will submit your labs individually.

Here are your assigned groups for the semester.

Goals

The primary goal of this lab is to give you lots of practice estimating and interpreting multiple regression models.

Questions 2-6 will all ask you to do some combination of the following:

  1. Fit a linear model or models using lm()
  2. Summarize the results of this model using summary()
  3. Present the results of this model or models in a regression table
  4. Interpret your models substantively for other human beings

Question 2 will also give you practice visualizing bivariate relationships

In general, when we interpret the regression coefficients from a linear model we want to know their:

  • Sign is the coefficient positive or negative? As the predictor increases does the outcome tend to increase (positive) or decrease (negative)
  • Size is the change in the predicted value of the outcome substantively meaningful?
    • To facilitate comparisons between predictors, we will use standardized measures of Republican Vote Share, Median Age, and Median Income, and Percent Vaccinated
  • Significance today we’ll put the cart before the horse, and say, coefficient that has one or more asterisks * next to it is statistically significant
    • Over the next several weeks, we’ll talk in great detail the logic and theory behind statistical inference
    • For today, we’ll do a bit of “star-gazing” using these asterisks1 as heuristics to help us evaluate the claims of Leonhardt and his skeptics.

Workflow

Please knit this .qmd file

As with every lab, you should:

  • Download the file
  • Save it in your course folder
  • Update the author: section of the YAML header to include the names of your group members in attendance.
  • Render the document
  • Open the html file in your browser (Easier to read)
  • Write your code in the chunks provided under each section
  • Comment out or delete any test code you do not need
  • Render the document again after completing a section or chunk (Error checking)
  • Upload the final lab to Canvas.

1 Get setup to work

1.1 Load Packages

First lets load the libraries we’ll need for today.

There’s one new package, htmltools which we’ll use to display regression tables while we work.

the_packages <- c(
  ## R Markdown
  "kableExtra","DT","texreg","htmltools",
  ## Tidyverse
  "tidyverse", "lubridate", "forcats", "haven", "labelled",
  ## Extensions for ggplot
  "ggmap","ggrepel", "ggridges", "ggthemes", "ggpubr", 
  "GGally", "scales", "dagitty", "ggdag", "ggforce",
  # Data 
  "COVID19","maps","mapdata","qss","tidycensus", "dataverse",
  # Analysis
  "DeclareDesign", "easystats", "zoo"
)

# Define function to load packages
ipak <- function(pkg){
    new.pkg <- pkg[!(pkg %in% installed.packages()[, "Package"])]
    if (length(new.pkg)) 
        install.packages(new.pkg, dependencies = TRUE)
    sapply(pkg, require, character.only = TRUE)
}

ipak(the_packages)
   kableExtra            DT        texreg     htmltools     tidyverse 
         TRUE          TRUE          TRUE          TRUE          TRUE 
    lubridate       forcats         haven      labelled         ggmap 
         TRUE          TRUE          TRUE          TRUE          TRUE 
      ggrepel      ggridges      ggthemes        ggpubr        GGally 
         TRUE          TRUE          TRUE          TRUE          TRUE 
       scales       dagitty         ggdag       ggforce       COVID19 
         TRUE          TRUE          TRUE          TRUE          TRUE 
         maps       mapdata           qss    tidycensus     dataverse 
         TRUE          TRUE          TRUE          TRUE          TRUE 
DeclareDesign     easystats           zoo 
         TRUE          TRUE          TRUE

1.2 Load the data

Next we’ll load the data that we created in class on Tuesday which provides a snapshot of the state of Covid-19 on September 23, 2021 in the U.S.

load(url("https://pols1600.paultesta.org/files/data/06_lab.rda"))

After running this code, the data frame covid_lab should appear in your environment pane in R Studio

1.3 Describe the data

In the code chunk below, please write some code get an high level overview of the data:

# High level overview
# Number of observations and variables
dim(covid_lab)
[1] 51 14
# Names of variables
names(covid_lab)
 [1] "state"                  "state_po"               "date"                  
 [4] "new_deaths_pc_14day"    "percent_vaccinated"     "winner"                
 [7] "rep_voteshare"          "med_age"                "med_income"            
[10] "population"             "rep_voteshare_std"      "med_age_std"           
[13] "med_income_std"         "percent_vaccinated_std"
# Glimpse of data
glimpse(covid_lab)
Rows: 51
Columns: 14
$ state                  <chr> "Minnesota", "California", "Florida", "Wyoming"…
$ state_po               <I<chr>> MN, CA, FL, WY, SD, KS, NV, VA, WA, OR, WI, …
$ date                   <date> 2021-09-23, 2021-09-23, 2021-09-23, 2021-09-23…
$ new_deaths_pc_14day    <dbl> 0.2216457, 0.2953878, 1.6069796, 0.9379675, 0.2…
$ percent_vaccinated     <dbl> 60.97676, 60.75909, 58.42173, 43.87526, 52.3523…
$ winner                 <fct> Biden, Biden, Trump, Trump, Trump, Trump, Biden…
$ rep_voteshare          <dbl> 45.28494, 34.32072, 51.21982, 69.49979, 61.7693…
$ med_age                <dbl> 38.0, 36.5, 42.0, 37.7, 37.0, 36.7, 38.0, 38.2,…
$ med_income             <dbl> 71306, 75235, 55660, 64049, 58275, 59597, 60365…
$ population             <int> 5639632, 39512223, 21477737, 578759, 884659, 29…
$ rep_voteshare_std      <dbl> -0.322498636, -1.235628147, 0.171773837, 1.6941…
$ med_age_std            <dbl> -0.16122563, -0.78101262, 1.49153966, -0.285183…
$ med_income_std         <dbl> 0.76603213, 1.13270974, -0.69414553, 0.08876578…
$ percent_vaccinated_std <dbl> 0.5889289, 0.5623160, 0.2765518, -1.5018949, -0…
# Summary of data
summary(covid_lab)
    state             state_po              date            new_deaths_pc_14day
 Length:51          Length:51          Min.   :2021-09-23   Min.   :0.08097    
 Class :character   Class :AsIs        1st Qu.:2021-09-23   1st Qu.:0.25590    
 Mode  :character   Mode  :character   Median :2021-09-23   Median :0.37909    
                                       Mean   :2021-09-23   Mean   :0.56561    
                                       3rd Qu.:2021-09-23   3rd Qu.:0.85135    
                                       Max.   :2021-09-23   Max.   :1.81515    
 percent_vaccinated   winner   rep_voteshare       med_age        med_income   
 Min.   :43.58      Trump:25   Min.   : 5.397   Min.   :30.80   Min.   :45081  
 1st Qu.:49.40      Biden:26   1st Qu.:40.975   1st Qu.:36.95   1st Qu.:55560  
 Median :54.65                 Median :49.237   Median :38.20   Median :61439  
 Mean   :56.16                 Mean   :49.157   Mean   :38.39   Mean   :63098  
 3rd Qu.:62.07                 3rd Qu.:57.866   3rd Qu.:39.50   3rd Qu.:71464  
 Max.   :72.39                 Max.   :69.500   Max.   :44.70   Max.   :86420  
   population       rep_voteshare_std    med_age_std       med_income_std   
 Min.   :  578759   Min.   :-3.644447   Min.   :-3.13620   Min.   :-1.6814  
 1st Qu.: 1789606   1st Qu.:-0.681443   1st Qu.:-0.59508   1st Qu.:-0.7034  
 Median : 4467673   Median : 0.006679   Median :-0.07859   Median :-0.1548  
 Mean   : 6445656   Mean   : 0.000000   Mean   : 0.00000   Mean   : 0.0000  
 3rd Qu.: 7446805   3rd Qu.: 0.725319   3rd Qu.: 0.45856   3rd Qu.: 0.7807  
 Max.   :39512223   Max.   : 1.694179   Max.   : 2.60716   Max.   : 2.1766  
 percent_vaccinated_std
 Min.   :-1.5381       
 1st Qu.:-0.8265       
 Median :-0.1841       
 Mean   : 0.0000       
 3rd Qu.: 0.7230       
 Max.   : 1.9845       
# Variables I want to calculate sd for
the_vars <- c("new_deaths_pc_14day","rep_voteshare","med_age","med_income","percent_vaccinated")

# Calculate standard deviations
covid_lab %>%
  select(all_of(the_vars))%>%
  summarise_all(sd)
# A tibble: 1 × 5
  new_deaths_pc_14day rep_voteshare med_age med_income percent_vaccinated
                <dbl>         <dbl>   <dbl>      <dbl>              <dbl>
1               0.409          12.0    2.42     10715.               8.18

Please use this HLO to answer the following questions:

  • How many observations are there: 50

  • What is an observation (i.e. what is the unit of analysis): A U.S. State (on September 23, 2021)

  • What is the primary outcome variable for today: The 14-day average of new Covid-19 deaths

  • What are the four main predictors we’ll be using: We’ll be predicting Covid-19 deaths with measures of Republican Vote Share (rep_voteshare), Median Age (med_age), Median Income (med_income), and Percent Vaccintated (percent_vaccinated).

  • Will we be using the the raw values of these predictors or their standardized values? We’ll be using the standardized version of these variables which all have the suffix _std

  • What are the standard deviations of our outcome and predictor variables:

    • Covid-19 deaths: 0.40 deaths
    • Republican vote share: 10.4 percentage points
    • Median age: 2.36 years
    • Median income: $ 10,288
    • Vaccination Rate: 7.98 percentage points

2 Estimate and interpet the baseline Red Covid model

First let’s estimate and interpret the following model:

\[\text{New Covid Deaths} = \beta_0 + \beta_1 \text{Republican Vote Share}_{std} + \epsilon\]

All you have to do is run the code chunks below and then interpret the results

When you visualize this model, you will have to write comments in the code

Then, you’ll use this code as guide for subsequent sections.

2.1 Fit the model

m1 <- lm(new_deaths_pc_14day ~ rep_voteshare_std, covid_lab)

2.2 Summarize the results

Now we apply the summary() function to our model m1

summary(m1)

Call:
lm(formula = new_deaths_pc_14day ~ rep_voteshare_std, data = covid_lab)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.63271 -0.22488 -0.03769  0.13746  1.00634 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        0.56561    0.04817  11.741 7.51e-16 ***
rep_voteshare_std  0.22682    0.04865   4.662 2.44e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.344 on 49 degrees of freedom
Multiple R-squared:  0.3073,    Adjusted R-squared:  0.2931 
F-statistic: 21.73 on 1 and 49 DF,  p-value: 2.44e-05

We see that m1 returns two coefficients, which define a line of best fit predicting Covid-19 deaths with the Republican vote share of the 2020 Presidential election:

  • \(\beta_0\) corresponds to the intercept. This is model’s prediction for a state where Trump got 0 percent of the vote. This is typically not something we care about.

  • \(\beta_1\) corresponds to the slope. Because we used a standardized measure of vote share, we would say that a 1-standard deviation (about 10 percentage points) increase in Republican vote share is associated with a 0.23 increase the average number of new Covid-19 deaths. Given that this per-capita measure has a standard deviation of 0.4, this is a fairly sizable association.

  • Finally, note that last column of summary(m1) Pr(>|t|) both the coefficients for the intercept \((\beta_0)\) and rep_voteshare_std (\((\beta_1)\)) are statistically significant (ie have an * next to them).

2.3 Display the model as a regression table

Next we’ll format the results of summary(m1) into a regression table using the htmlreg() function.

Regression tables are a the standard way of concisely presenting the results of regression models.

  • Each named row corresponds to the coefficients form the model

  • If there is an asterisks next to a coefficient, that coefficient is statistically significant with a p value below a certain threshold.

  • The numbers in parentheses below each coefficient correspond to the standard error of the coefficient (more on that later)2

  • The bottom of the table contains summary statistics of of our model, which we’ll ignore for today.

The code after htmlreg(m1) allows you to see what output of the table will look like in the html document while you’re working in the Rmd file.

Statistical models
  Model 1
(Intercept) 0.57***
  (0.05)
rep_voteshare_std 0.23***
  (0.05)
R2 0.31
Adj. R2 0.29
Num. obs. 51
***p < 0.001; **p < 0.01; *p < 0.05

2.4 Visualize the model

Now let’s visualize the results of our m1 with a scatter plot.

In the code chunk below, I’ve written some comments to help you get started. You can also refer to last week’s lab for help

# 1. Tell ggplot what data to use
covid_lab %>%
# 2. Set the aesthetic mappings of our figure
  ggplot(aes(x = rep_voteshare_std,
             y = new_deaths_pc_14day,
             label = state_po))+
# 3. Draw points with x values corresponding to Rep vote share and y values corresponding to Covid deaths. 
  geom_point(
# 4. Make the points smaller in size
    size = .5
    )+
# 5. Add labels using `label=state_po` aesthetic 
  geom_text_repel(
# 6. Make the label size smaller    
    size = 2)+
# 7. Plot the regression model
  geom_smooth(method = "lm")+
# 8. Change the axis labels
  labs(
    x = "Republican Vote Share (std)",
    y = "New Covid-19 Deaths\n(14-day ave)"
  )

2.5 Interpret the results

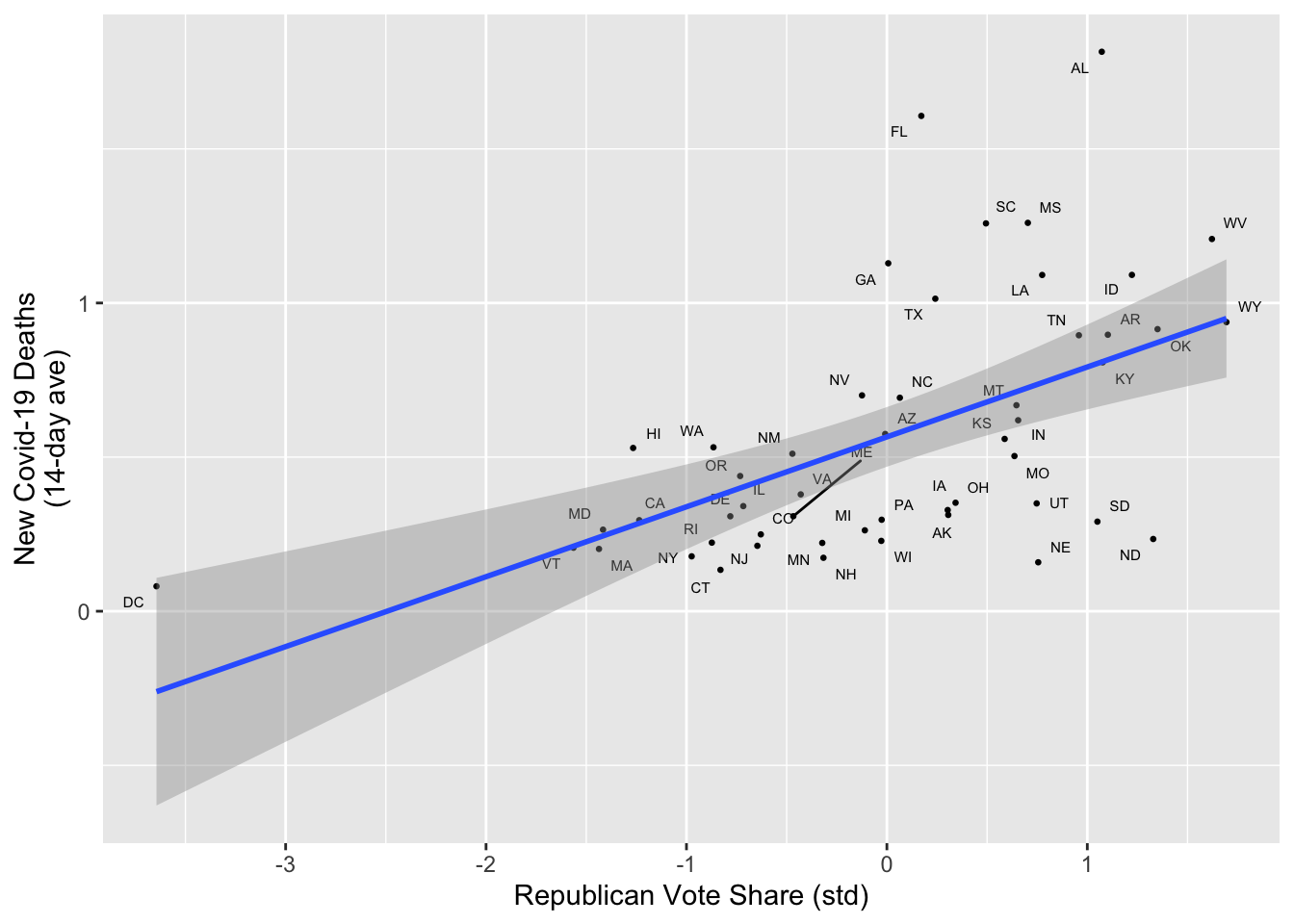
In a sentence our two, summarize the results of your analysis in this section

Our model in this section provides results consistent with the phenomena of Red Covid. State’s with higher Republican vote shares tended to have higher per capita rates of death from Covid-19 on September 23, 2022.

3 Estimate a model controlling for age

Suppose a skeptic reading the New York Times took issue with Leonhardt’s claims, and said what’s really behind the claim of Red Covid is that Republican states tend to be older and older people are more at Risk of Dying from Covid-19.

One way we could address this critique is by estimating a multiple regression model that controlled for age.

\[\text{New Covid Deaths} = \beta_0 + \beta_1 \text{Repbulican Vote Share}_{std} + \beta_2 \text{Median Age}_{std} + \epsilon\]

If our skeptic is right, what should happen to coefficients:

  • Republican Vote Share:
    • Sign: Unclear
    • Size: Decrease compared m1
    • Significance: Non-Significant
  • Median Age:
    • Sign: Positive
    • Size: Unclear
    • Significance: Significant

If our critique is right, and the relationship between Partisanship and Covid is confounded by the fact that Red States tend to be older and older people are more likely to die from Covid, then controlling for Age, the coefficient on Republican Vote share should decrease in size (get closer to 0) and lose significance, while the coefficient on Age should be positive (older states have more Covid-19 deaths) and statistically signficant. I’m not sure I have a good sense about the size or magnitude of this effect.

3.1 Fit the model

Now let’s test our skeptics’ claims by fitting a model m2 that controls for Age (med_age_std).

  • Remember the first argument in lm() is formula of the form outcome variable ~ predictor1 + predictor2 + ...
m2 <- lm(new_deaths_pc_14day ~ rep_voteshare_std + med_age_std, covid_lab)

3.2 Summarize the model

Now let’s print out a statistical summary of m2

summary(m2)

Call:
lm(formula = new_deaths_pc_14day ~ rep_voteshare_std + med_age_std, 
    data = covid_lab)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.59508 -0.24816 -0.05547  0.13825  0.99419 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        0.56561    0.04847  11.670 1.27e-15 ***
rep_voteshare_std  0.23074    0.04933   4.677 2.40e-05 ***
med_age_std        0.03152    0.04933   0.639    0.526    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3461 on 48 degrees of freedom
Multiple R-squared:  0.3131,    Adjusted R-squared:  0.2845 
F-statistic: 10.94 on 2 and 48 DF,  p-value: 0.0001218

3.3 Display the model as a regression table

Next, let’s create a regression table that displays m1 in the first column and m2 in the second column.

  • To do this, change list(m1) from the code above to list(m1, m2)
Statistical models
  Model 1 Model 2
(Intercept) 0.57*** 0.57***
  (0.05) (0.05)
rep_voteshare_std 0.23*** 0.23***
  (0.05) (0.05)
med_age_std   0.03
    (0.05)
R2 0.31 0.31
Adj. R2 0.29 0.28
Num. obs. 51 51
***p < 0.001; **p < 0.01; *p < 0.05

3.4 Interpret the results

In a few sentences, explain whether the results from m2 support the skeptics criticisms or not?

  • They do not. Controlling for differences in the median age of state’s population does little to change the relationship between partisanship and Covid-19 that we saw in m1. If anything the the relationship is slightly stronger, while the coefficient on age is substantively small and statistically non-significant.

Part of what’s at play here, is that relationship between age and Covid-19 outcomes at the state level is pretty weak, perhaps reflecting the early focus on vaccinating the eldery.

Similarly, the idea that Red States tend to be older doesn’t appear to be empirically true, perhaps reflecting differences between the general population and voting population.

# Fit models
m2_death_age <- lm(new_deaths_pc_14day ~ med_age_std, covid_lab)
m2_rep_age <- lm(rep_voteshare_std ~ med_age_std, covid_lab)

# Summarize models
summary(m2_death_age)

Call:
lm(formula = new_deaths_pc_14day ~ med_age_std, data = covid_lab)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.4796 -0.3095 -0.1863  0.2853  1.2488 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.565611   0.057879   9.772  4.3e-13 ***
med_age_std 0.002763   0.058454   0.047    0.962    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4133 on 49 degrees of freedom
Multiple R-squared:  4.56e-05,  Adjusted R-squared:  -0.02036 
F-statistic: 0.002234 on 1 and 49 DF,  p-value: 0.9625
summary(m2_rep_age)

Call:
lm(formula = rep_voteshare_std ~ med_age_std, data = covid_lab)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.8705 -0.6764  0.0464  0.6577  1.8335 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.883e-16  1.403e-01   0.000    1.000
med_age_std -1.246e-01  1.417e-01  -0.879    0.384

Residual standard error: 1.002 on 49 degrees of freedom
Multiple R-squared:  0.01553,   Adjusted R-squared:  -0.004562 
F-statistic: 0.7729 on 1 and 49 DF,  p-value: 0.3836
# Display as formatted regression table
htmlreg(list(m2_rep_age,
             m2_death_age),
        custom.model.names = c("Deaths", "Rep Vote"),
        custom.coef.names = c("(Intercept)","Median Age (std)"),
        custom.header = list("DV"=1:2)  )%>% HTML() %>% browsable()
Statistical models
  DV
  Deaths Rep Vote
(Intercept) -0.00 0.57***
  (0.14) (0.06)
Median Age (std) -0.12 0.00
  (0.14) (0.06)
R2 0.02 0.00
Adj. R2 -0.00 -0.02
Num. obs. 51 51
***p < 0.001; **p < 0.01; *p < 0.05 
# Visualize the models
covid_lab %>%
  ggplot(aes(x = med_age_std,
             y = rep_voteshare_std,
             label = state_po))+
  geom_point(size = .5)+
  geom_text_repel(size = 2)+
  geom_smooth(method = "lm")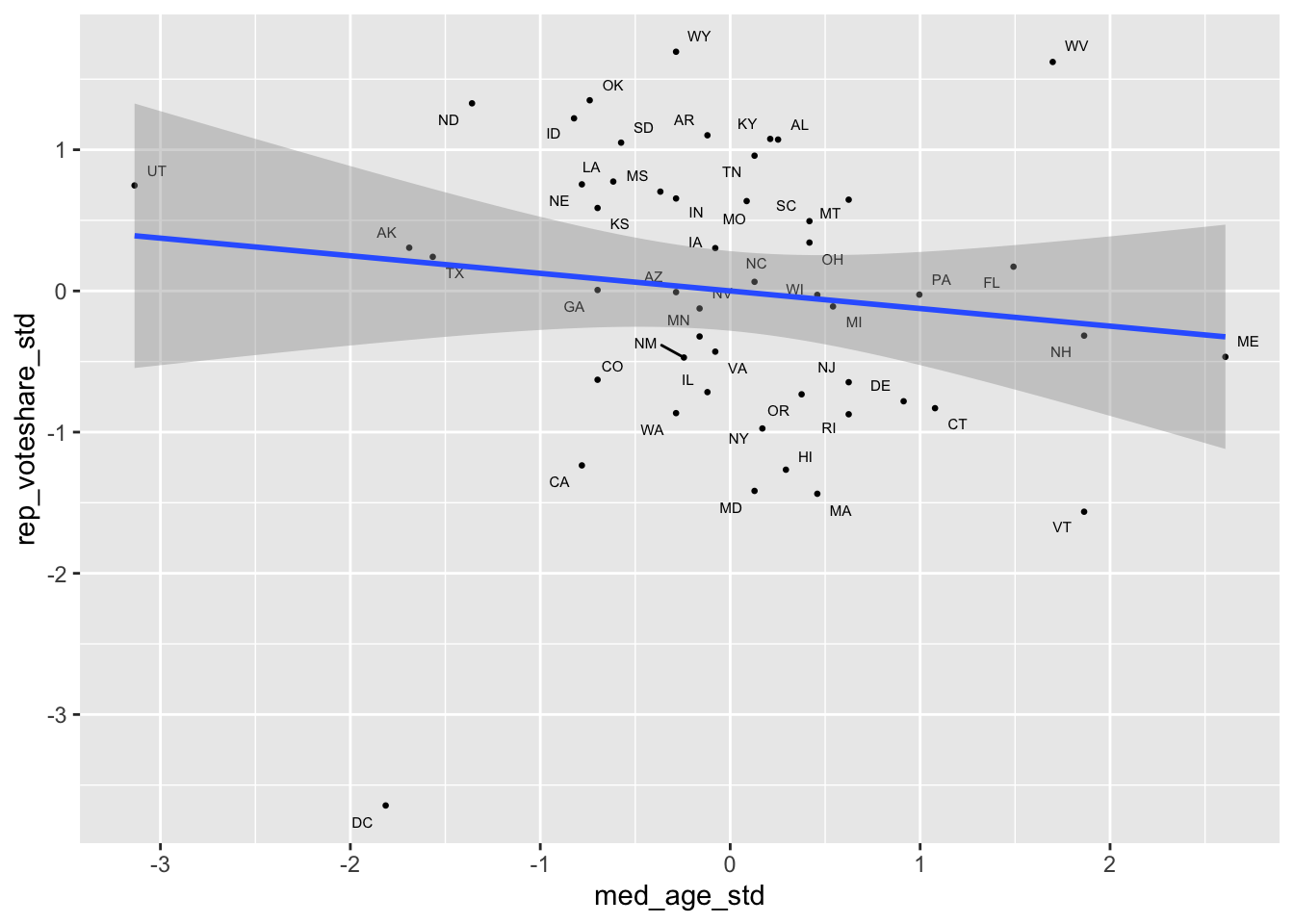

covid_lab %>%
  ggplot(aes(x = med_age_std,
             y = new_deaths_pc_14day,
             label = state_po))+
  geom_point(size = .5)+
  geom_text_repel(size = 2)+
  geom_smooth(method = "lm")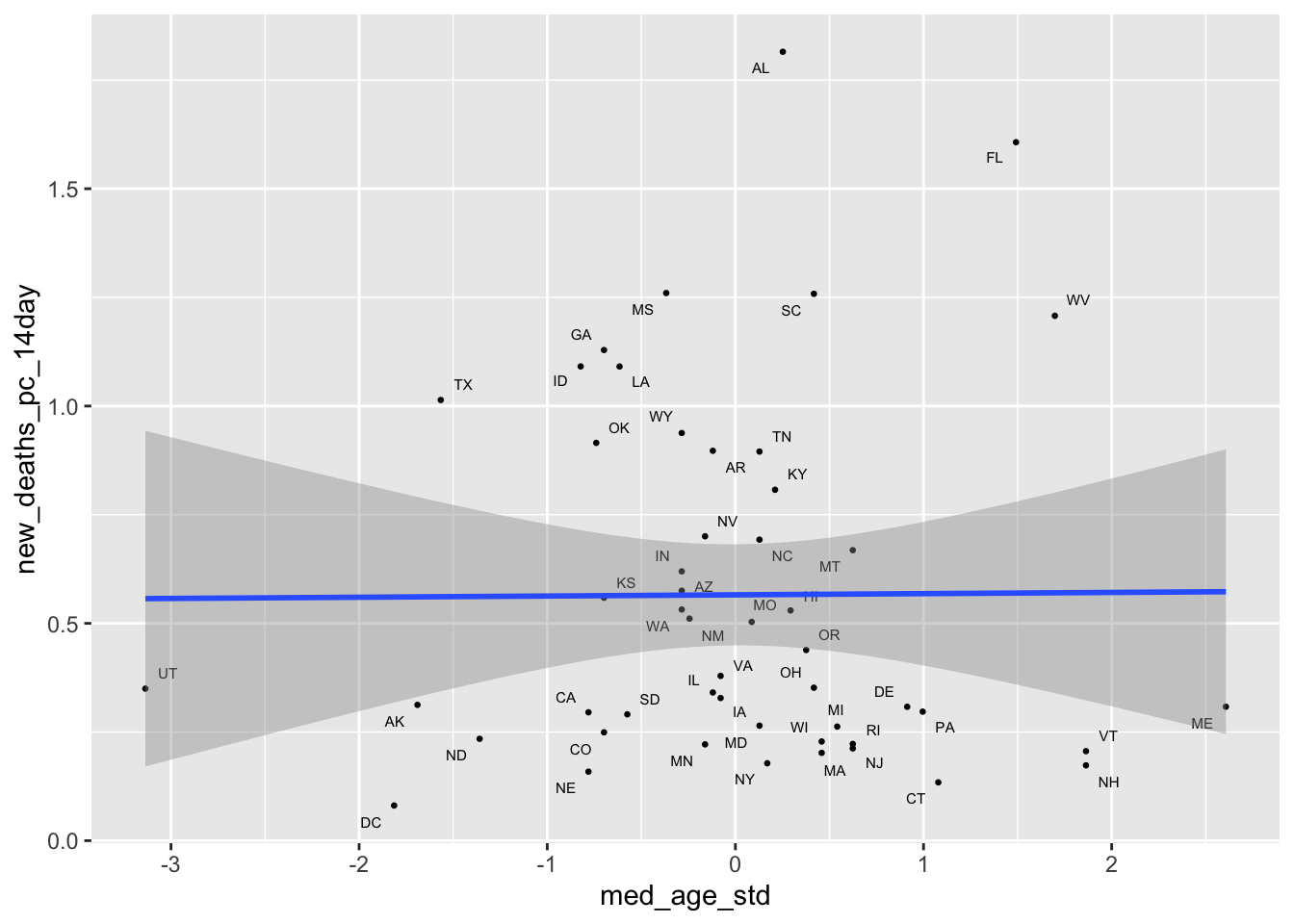

4 Estimate a model controlling for age and income

Undeterred, our skeptic now argues that it’s not just age that matters but also socioeconomic factors like wealth.

Let’s test this claim using the following model:

\[\text{New Covid Deaths} = \beta_0 + \beta_1 \text{Repbulican Vote Share}_{std} + \beta_2 \text{Median Age}_{std} + \beta_3\text{Median Income}_{std}\epsilon\]

If the skeptic is right, then controlling for age and income, the coefficient on Republican vote share should decrease in size and no longer be statistically significant

4.1 Fit the Model

Please fit a model called m3 implied by the skeptic’s revised claims

m3 <- lm(new_deaths_pc_14day ~ rep_voteshare_std + med_age_std + med_income_std, covid_lab)

4.2 Summarize the model

Summarize the model m3 using summary()

summary(m3)

Call:
lm(formula = new_deaths_pc_14day ~ rep_voteshare_std + med_age_std + 
    med_income_std, data = covid_lab)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.50751 -0.19703 -0.06278  0.20024  0.92320 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        0.56561    0.04425  12.782  < 2e-16 ***
rep_voteshare_std  0.07140    0.06654   1.073  0.28869    
med_age_std       -0.01692    0.04744  -0.357  0.72296    
med_income_std    -0.21669    0.06660  -3.254  0.00211 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.316 on 47 degrees of freedom
Multiple R-squared:  0.4394,    Adjusted R-squared:  0.4036 
F-statistic: 12.28 on 3 and 47 DF,  p-value: 4.689e-06

4.3 Display the models in a regression table

And then display the results of models m1, m2, and m3.

htmlreg(list(m1,m2,m3)) %>% HTML() %>% browsable()
Statistical models
  Model 1 Model 2 Model 3
(Intercept) 0.57*** 0.57*** 0.57***
  (0.05) (0.05) (0.04)
rep_voteshare_std 0.23*** 0.23*** 0.07
  (0.05) (0.05) (0.07)
med_age_std   0.03 -0.02
    (0.05) (0.05)
med_income_std     -0.22**
      (0.07)
R2 0.31 0.31 0.44
Adj. R2 0.29 0.28 0.40
Num. obs. 51 51 51
***p < 0.001; **p < 0.01; *p < 0.05

4.4 Interpret the skeptic’s claims

In a few sentences, explain whether the results from m3 support the skeptics criticisms or not?

Controlling for median age and income, the coefficient on Republican sote share decreases in size by more than half and is no longer statistically significant. The coefficient on median income is statistically significant and substantively suggests that states with higher median incomes tended to have fewer Covid-19 deaths on September 23, 2021.

5 Estimate a model controlling for age, income, and percent vaccinated

Hmm, maybe our skeptic has a point. Let’s estimate a model that controls for everything from m3 as well as the vaccination rate in each state.

\[\text{New Covid Deaths} = \beta_0 + \beta_1 \text{Rep Vote Share}_{std} + \beta_2 \text{Median Age}_{std} + \beta_3\text{Median Income}_{std}+\beta_4\text{Percent Vaxxed}_{std}\epsilon\]

5.1 Fit the model

You know the drill.

m4 <- lm(new_deaths_pc_14day ~ rep_voteshare_std + med_age_std + med_income_std + percent_vaccinated_std, covid_lab)

5.2 Summarize the results

Again, let’s get a quick summary of our results

summary(m4)

Call:
lm(formula = new_deaths_pc_14day ~ rep_voteshare_std + med_age_std + 
    med_income_std + percent_vaccinated_std, data = covid_lab)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.52997 -0.16350 -0.02941  0.12926  0.94733 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)             0.56561    0.04091  13.825  < 2e-16 ***
rep_voteshare_std      -0.08933    0.08161  -1.095  0.27940    
med_age_std             0.07110    0.05278   1.347  0.18458    
med_income_std         -0.11888    0.06969  -1.706  0.09478 .  
percent_vaccinated_std -0.28633    0.09554  -2.997  0.00438 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2922 on 46 degrees of freedom
Multiple R-squared:  0.531, Adjusted R-squared:  0.4902 
F-statistic: 13.02 on 4 and 46 DF,  p-value: 3.621e-07

5.3 Display the models in a regression table

And add m4 to list of models in our regression table

Statistical models
  Model 1 Model 2 Model 3 Model 4
(Intercept) 0.57*** 0.57*** 0.57*** 0.57***
  (0.05) (0.05) (0.04) (0.04)
rep_voteshare_std 0.23*** 0.23*** 0.07 -0.09
  (0.05) (0.05) (0.07) (0.08)
med_age_std   0.03 -0.02 0.07
    (0.05) (0.05) (0.05)
med_income_std     -0.22** -0.12
      (0.07) (0.07)
percent_vaccinated_std       -0.29**
        (0.10)
R2 0.31 0.31 0.44 0.53
Adj. R2 0.29 0.28 0.40 0.49
Num. obs. 51 51 51 51
***p < 0.001; **p < 0.01; *p < 0.05

5.4 Interpet the results

Briefly interpret the results of m4

Controlling for vaccination rates, none of the other variables in m4 are statistically significant predictors of Covid-19 deaths.

6 Model percent vaccinated in a state controlling for age, income, and republican vote share

Hmm, how should we make sense of m4. Let’s fit one last model, that predicts vaccination rates as a function of Republican vote share, median age, and median income in a state.

\[\text{Percent Vaxxed} = \beta_0 + \beta_1 \text{Repbulican Vote Share}_{std} + \beta_2 \text{Median Age}_{std} + \beta_3\text{Median Income}_{std}\epsilon\] Briefly, please describe whether we should expect a statistically significant positive or negative relationship with vaccination rates or whether we should expect no statistically significant relationship.

  • \(\beta_1\) Republican Vote Share: Negative

  • \(\beta_2\) Median Age: Positive

  • \(\beta_3\) Median Income: Positive

6.1 Fit the model

Now let’s fit the model. For ease of interpretation, let’s use the unstandardized measure of vaccination rates, percent_vaccinated as our outcome variable.

m5 <- lm(percent_vaccinated ~ rep_voteshare_std + med_age_std + med_income_std, covid_lab)

6.2 Summarize the results

And summarize the results

summary(m5)

Call:
lm(formula = percent_vaccinated ~ rep_voteshare_std + med_age_std + 
    med_income_std, data = covid_lab)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7719 -2.7849  0.2386  1.7743  7.6442 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)        56.1597     0.5109 109.919  < 2e-16 ***
rep_voteshare_std  -4.5916     0.7683  -5.977 2.92e-07 ***
med_age_std         2.5143     0.5477   4.590 3.31e-05 ***
med_income_std      2.7939     0.7690   3.633 0.000691 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.649 on 47 degrees of freedom
Multiple R-squared:  0.8129,    Adjusted R-squared:  0.801 
F-statistic: 68.09 on 3 and 47 DF,  p-value: < 2.2e-16

6.3 Display the results in a regression table

Display them in a regression table

Statistical models
  Model 1
(Intercept) 56.16***
  (0.51)
rep_voteshare_std -4.59***
  (0.77)
med_age_std 2.51***
  (0.55)
med_income_std 2.79***
  (0.77)
R2 0.81
Adj. R2 0.80
Num. obs. 51
***p < 0.001; **p < 0.01; *p < 0.05

6.4 Interpret the results

Summarize the results of m5 and offer some broader discussion of what we’ve learned today

In m5 all three predictors have strong statistically significant relationships with vaccination rates in the expected direction. States where more people voted for Trump in 2020 tend to have lower rates of vaccination. States with an older population, and a richer population tend to have higher rates of vaccination.

Thinking back to the previous models we’ve estimated, we might argue that the effects these predictors have on Covid-19 death rates is mediated through their relationship with vaccination rates.

More broadly, what does this analysis mean for arguments about Red Covid. I guess, I’d say it’s complicated. Vaccines are clearly effective at reducing Covid-19 deaths. In both aggregate and invidual level data, Republicans appear to be less willing to get vaccinated. But lots of other factors influence vaccination rates and public health more broadly.

Regression is a tool for trying to explore these competing explanations, but without strong theory and clever design, it’s unlikely to resolve debates. There’s almost always a skeptic waiting to say “Yes, but have you controlled for …” We can try to address there concerns by controlling for more and more variables. But a better strategy is often to say, I don’t need to control for X because the logic of my design already accounts for X.

Still it’s hard to think what that kind of design would be for something like for debates about Red Covid. Maybe we need different (individual data) or maybe we’d want to reframe the question or draw out further testable implications of the claim. If your group is looking for a final project, there are number of directions you could take this kind of analysis:

  • Looking at different periods overtime
  • Looking at smaller units of aggregation (counties)
  • Controlling for alternative factors
  • Leveraging variation in the availability of vaccines over time and place.

Take the Class Survey

Please take a few moments to complete the class survey for this week.

Footnotes

  1. In short, these * correspond to \(p-values\) below different thresholds. One * typically means \(p < 0.05\). A p-value is a conditional probability that arises from a hypothesis test summarizing the likelihood of observing a particular test statistic (here a regression coefficient, or more specifically, a t-statistic which is the regression coefficient divided by its standard error) given a paritcular hypothesis (typically, but not allows a null hypothesis that the true coefficient is 0). In sum, a p-value assess the likelihood of seeing what we did, if in fact, there was no relationship. If that likelihood is small (p<0.05), we reject the claim of no relationship. We remain uncertain about the true value of the coefficient, but we are pretty confident it’s not 0.↩︎

  2. A standard error is another one of those things that in the cart we’re putting before horse today. Briefly, it is an estimate of the standard deviation of the sampling distribution of a coefficient and describes how much our coefficient might vary had we had a different sample…↩︎